题目内容
某商场购进一批单价为16元的日用品,销售一段时间后,经调查发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.若每月销售件数y(件)与价格x(元/件)满足关系式y=kx+b.
(1)确定y与x的函数关系式,并指出x的取值范围;
(2)为了使每月获得利润为1800元,问商品应定为每件多少元?
(1)确定y与x的函数关系式,并指出x的取值范围;
(2)为了使每月获得利润为1800元,问商品应定为每件多少元?
(1)根据题意得:
,
解得:
,
则y与x之间的函数关系式为:y=-30x+960.
(2)设利润M,则M与x的函数关系式是:
M=(-30x+960)(x-16).
即M=-30x2+1440x-15360
当M=1800时,即-30x2+1440x-15360=1800,
解方程得:x1=22,x2=26,
即为了获得1800元的利润,商品价格每件应定为22元或26元.
|
解得:
|
则y与x之间的函数关系式为:y=-30x+960.
(2)设利润M,则M与x的函数关系式是:
M=(-30x+960)(x-16).
即M=-30x2+1440x-15360
当M=1800时,即-30x2+1440x-15360=1800,
解方程得:x1=22,x2=26,
即为了获得1800元的利润,商品价格每件应定为22元或26元.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

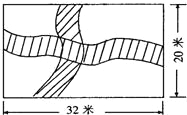
 一条等宽的小道.要使种植面积为540m2,小道的宽应是多少?
一条等宽的小道.要使种植面积为540m2,小道的宽应是多少?