题目内容
【题目】如图,AO=BO=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由A以2cm/s的速度向B爬行;同时另一只蚂蚁由O点以3cm/s的速度沿OC方向爬行.问:是否存在这样的时刻,使两只小蚂蚁与点O点组成的三角形面积为450cm2?

【答案】15s或10s或30s.
【解析】
可以分两种情况进行讨论:(1)当蚂蚁在AO上运动;(2)当蚂蚁在OB上运动.根据三角形的面积公式即可列方程求解.
有两种情况:
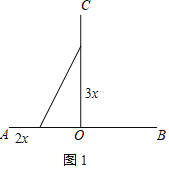
(1)如图1,当蚂蚁在AO上运动时,
设x秒后两只蚂蚁与O点组成的三角形面积为450cm2,
由题意,得:![]() ×3x×(50﹣2x)=450,
×3x×(50﹣2x)=450,
整理,得:x2﹣25x+150=0,
解得:x1=15,x2=10.
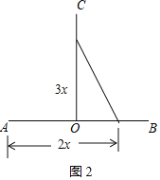
(2)如图2,当蚂蚁在OB上运动时,
设x秒钟后,两只蚂蚁与O点组成的三角形面积为450cm2,
由题意,得:![]() ×3x(2x﹣50)=450,
×3x(2x﹣50)=450,
整理,得:x2﹣25x﹣150=0,
解得x1=30,x2=﹣5(舍去).
答:15s,10s,30s后,两蚂蚁与O点组成的三角形的面积均为450cm2.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目