��Ŀ����
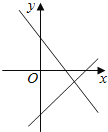
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����A������Ϊ����1��0������y�ύ�ڵ�C��0��3������ֱ��BC������P��x�����˶�������P��PM��x�ᣬ���������ڵ�M����ֱ��BC�ڵ�N�����P�ĺ�����Ϊm��
�������������ߵĽ���ʽ��ֱ��BC�Ľ���ʽ��
����������P���߶�OB���˶�ʱ�����߶�MN�����ֵ��
����������C��O��M��NΪ������ı�����ƽ���ı���ʱ��ֱ��д��m��ֵ��

���𰸡���1��y=��x2+2x+3��y=��x+3����2��![]() ����3��
����3��![]() ��
��![]()
�������������������1����A��C������������ߵĽ���ʽ���з���������b��c��ֵ����y=0���ⷽ�̿ɵ�B�����꣬���ô���ϵ������ֱ��BC�Ľ���ʽ��
��2�����ݽ���ʽ�ֱ��ʾM��N��������꣬��������IJ����MN�ij����䷽������ֵ���ɣ�
��3�������������������P���߶�OB��ʱ������MN=��m2+3m��������P�����߶�OB��ʱ������MN=��m+3������m2+2m+3��=m2��3m������MN=3�з��̽�����ɣ�
����������⣺��1���������߹�A��C���㣬�����������߽���ʽ�ɵã� ![]() ����ã�
����ã� ![]() ���������߽���ʽΪy=��x2+2x+3����y=0�ɵã���x2+2x+3=0����x1=��1��x2=3����B����A���Ҳ࣬��B������Ϊ��3��0������ֱ��BC����ʽΪy=kx+s����B��C�������ɵ���
���������߽���ʽΪy=��x2+2x+3����y=0�ɵã���x2+2x+3=0����x1=��1��x2=3����B����A���Ҳ࣬��B������Ϊ��3��0������ֱ��BC����ʽΪy=kx+s����B��C�������ɵ��� ![]() �������
������� ![]() ����ֱ��BC����ʽΪy=��x+3��
����ֱ��BC����ʽΪy=��x+3��
��2����PM��x�ᣬ��P�ĺ�����Ϊm����M��m����m2+2m+3����N��m����m+3������P���߶�OB���˶�����M����N���Ϸ�����MN=��m2+2m+3������m+3��=��m2+3m=����m��![]() ��2+
��2+![]() ������m=
������m=![]() ʱ��MN�����ֵ��MN�����ֵΪ
ʱ��MN�����ֵ��MN�����ֵΪ![]() ��
��
��3����PM��x�ᣬ��MN��OC������C��O��M��NΪ������ı�����ƽ���ı���ʱ������OC=MN������P���߶�OB��ʱ������MN=��m2+3m���ੁm2+3m=3���˷�����ʵ����������P�����߶�OB��ʱ������MN=��m+3������m2+2m+3��=m2��3m����m2��3m=3�����m=![]() ��m=
��m=![]() ��
��
���Ͽ�֪����C��O��M��NΪ������ı�����ƽ���ı���ʱ��m��ֵΪ![]() ��
��![]() ��
��