题目内容
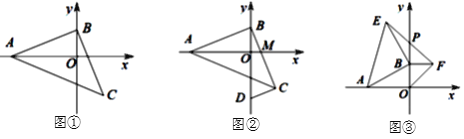
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
(1)按要求作图:
①以坐标原点O为旋转中心,将△ABC逆时针旋转90°得到△A1B1C1;
②作出△A1B1C1关于原点成中心对称的中心对称图形△A2B2C2.
(2)△A2B2C2中顶点B2坐标为 .

【答案】(1)见解析;(2)(1,6)
【解析】试题分析:
(1)①连接OA,过点O在第三象限作A1O⊥AO,使A1O=AO即可得到点A1,同法作出点B1、C1,再顺次连接A1、B1、C1即可;②连接A1O并延长到A2,使A2O=A1O即可得到点A2,同法作出点B2、C2,再顺次连接这三点即可.
(2)根据(1)中所画图形,写出点B2的坐标即可.
试题解析:
(1)①如下图所示:△A1B1C1,即为所求三角形;
②如下图所示:△A2B2C2,即为所求三角形;
(2)如下图,△A2B2C2中顶点B2坐标为:(1,6).
故答案为:(1,6).


练习册系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5