题目内容
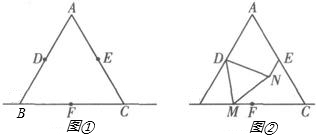
如图,已知等边三角形ABC中,点D、E、F分别为AB、AC、BC边的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).(1)如图①,当点M在BC边上时,求证:MF=NE.
(2)若点M在点B左侧,其他条件不变时,请你在图②中作出相应的图形(不写作法),MF与NE相等的结论是否仍然成立?请直接写出结论,不必证明或说明理由.
(3)请你利用(2)中所作出的图形来判断点F是否在直线NE上?并说明理由.
分析:(1)连接DE,DF,EF.根据三角形的中位线定理得到等边三角形DEF,再根据SAS证明△DMF≌△DNE,从而得到结论;
(2)类似(1)中的证明思路,显然结论仍然成立;
(3)连接DF,NF,EF.根据SAS证明△DBM≌△DFN,从而得到∠DFN=∠DBM=120°,再根据平角定义即可证明.
(2)类似(1)中的证明思路,显然结论仍然成立;
(3)连接DF,NF,EF.根据SAS证明△DBM≌△DFN,从而得到∠DFN=∠DBM=120°,再根据平角定义即可证明.
解答: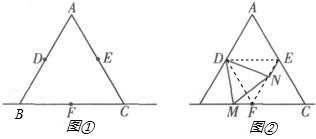 (1)证明:连接DE,DF,EF.(1分)
(1)证明:连接DE,DF,EF.(1分)
∵△ABC是等边三角形,
∴AB=AC=BC.
又∵DE,DF,EF为三角形的中位线.
∴DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,
∴∠MDF=∠NDE.(3分)
又∵DM=DN,
∴△DMF≌△DNE.(4分)
∴MF=NE.(5分)
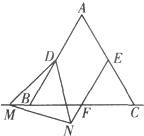
(2)画出图形(如答图).(7分)
MF与NE相等的结论仍然成立.(8分)
(3)点F在直线NE上.(9分)
连接DF,NF,EF.
由(1),知DF=
AC=
AB=DB.
又∠BDM+∠BDN=60°,∠NDF+∠BDN=60°,
∴∠BDM=∠NDF,
又∵DM=DN,
∴△DBM≌△DFN.(10分)
∴∠DFN=∠DBM=120°.
又∵∠DFE=60°.
∴∠NFE=∠DFN+∠DFE=180°.(11分)
可得点F在NE上.(12分)
 (1)证明:连接DE,DF,EF.(1分)
(1)证明:连接DE,DF,EF.(1分)∵△ABC是等边三角形,
∴AB=AC=BC.
又∵DE,DF,EF为三角形的中位线.
∴DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,
∴∠MDF=∠NDE.(3分)
又∵DM=DN,
∴△DMF≌△DNE.(4分)
∴MF=NE.(5分)

(2)画出图形(如答图).(7分)
MF与NE相等的结论仍然成立.(8分)
(3)点F在直线NE上.(9分)
连接DF,NF,EF.
由(1),知DF=
| 1 |
| 2 |
| 1 |
| 2 |
又∠BDM+∠BDN=60°,∠NDF+∠BDN=60°,
∴∠BDM=∠NDF,
又∵DM=DN,
∴△DBM≌△DFN.(10分)
∴∠DFN=∠DBM=120°.
又∵∠DFE=60°.
∴∠NFE=∠DFN+∠DFE=180°.(11分)
可得点F在NE上.(12分)
点评:此题综合运用了等边三角形的性质和判定、全等三角形的判定和性质.全等是证明线段相等的常用方法,证明三点共线的方法是利用平角定义.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.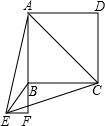 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想. 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动