题目内容
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
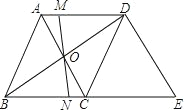
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
【答案】(1) OM=ON.(2)24.
【解析】
试题分析:(1)根据四边形ABCD是菱形,判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=5,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少.
试题解析:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴![]() =1,
=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=5,
∴BO=![]() =4,
=4,
∴BD=2BO=8,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=8+6+(5+5)
=24
即△BDE的周长是24.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目