题目内容
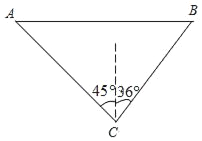
【题目】如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:![]() ≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0. 727,cot36°≈1.376)
≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0. 727,cot36°≈1.376)
【答案】A、B之间的距离为279米.
【解析】试题分析:本题可通过构建直角三角形来解答,过点C作AB的垂线交AB于H,要先求出CH的值然后再求AH,BH的值,进而得出AB的长.
试题解析:
过点C作CH⊥AB,垂足为点H,
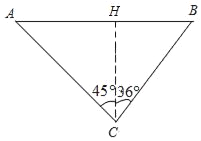
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,![]() ,
,
∴![]() ,
,
∵sin36°≈0.588,
∴BH≈117.6,
又![]() ,
,
∴![]() .
.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,![]() ,
,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目