题目内容
【题目】如图，坐标平面里的图像表示一汽车从甲地到乙地时间x与路程y之间的函数关系，横线表示停车修理．
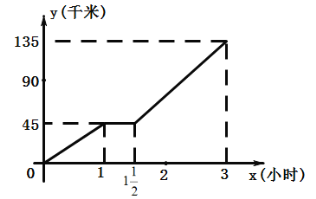
（1）根据图像回答下列问题：前1小时汽车的速度是多少千米／时；停车修理的时间为多少？；后
小时汽车的速度是多少千米/时？甲、乙两地相距多少千米？
（2）适当选取图像中所给的数据，编一个一元一次方程应用题，并列出方程（不要求解）
【答案】（1）45km/h；
小时；60km/h；135千米；（2）问：汽车何时离甲地的距离为100千米？所列方程为：
【解析】
（1）根据前1小时的路程是45千米即可求出速度，由图象即可得出修理的时间，根据路程为（135-45）千米，即可求出后
小时汽车的速度，由图象即可得甲、乙两地相距多少千米；
（2）根据图象，编写应用题：汽车何时离甲地的距离为100千米？列出方程即可．
解：（1）前1小时汽车的速度是
（km/h）；
停车修理的时间为
（小时）；
后小时汽车的速度是
（km/h）；
甲、乙两地相距135千米；
（2）问：汽车何时离甲地的距离为100千米？
设汽车出发后x小时后离甲地的距离为100千米，
则．
一本好题口算题卡系列答案【题目】某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：
销售单价x（元） | 85 | 95 | 105 | 115 |
日销售量y（个） | 175 | 125 | 75 | m |
日销售利润w（元） | 875 | 1875 | 1875 | 875 |
（注：日销售利润=日销售量×（销售单价﹣成本单价））
（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；
（2）根据以上信息，填空：
该产品的成本单价是 元，当销售单价x= 元时，日销售利润w最大，最大值是 元；
（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？
【题目】某单位要将一份宣传资料进行批量印刷．在甲印刷厂，在收取100元制版费的基础上，每份收费0.5元；在乙印刷厂，在收取40元侧版费的基础上，每份收费0.7元．设该单位要印刷此宣传资料
份（为正整数）．
（Ⅰ）根据题意，填写下表：
印剧数量（份） | 150 | 250 | 350 | 450 | … |
甲印刷厂收费（元） | 175 | ① | 275 | ② | … |
乙印刷厂收费（元） | 145 | 215 | ③ | 355 | … |
（Ⅱ）设在甲印刷厂收费
元，在乙印刷厂收费
元，分别写出，关于的函数解析式；
（Ⅲ）当
时，在哪家印刷厂花费少？请说明理由．
