Question

如图①，已知抛物线y= ax²+bx+ c经过坐标原点，与x轴的另一个交点为A，且顶点M坐标为（1，2），

 

 

（1）求该抛物线的解析式；

（2）现将它向右平移m(m＞0)个单位，所得抛物线与x轴交于C、D两点，与原抛物线交于点P，△CDP

的面积为S，求S关于m的关系式；

（3）如图②，以点A为圆心，以线段OA为半径画圆，交抛物线y = ax²+bx+ c的对称轴于点B，连结AB，若将抛物线向右平移m(m＞0)个单位后，B点的对应点为B′，A点的对应点为A′点，且满足四边形为菱形，平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,使得以E、F、A′为顶点的三角形与△BAE相似，若存在求出F点坐标，若不存在说明理由.

 

 

 

Answer 1

 

 抛物线y = ax²+bx+ c顶点M坐标为（1,2），

设二次函数解析式为

（*）

抛物线y = ax²+bx+ c经过坐标原点，

把（0,0）代入（*）式得：

二次函数解析式为

 

由题意知A点坐标为（2，0）

当0<m<2时，如图1，作PH⊥x轴于点H，设,

 

∵抛物线向右平移m个单位

∴A（2，0），C（m,0）,

∴AC=2-m, ∴CH= ，

∴=OH= =.

 

 

 

根据题意可知：,

根据勾股定理得：

根据三角函数定义知道：

可求得：;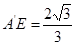

设=

（1） 当

∽

 

 

 解析:略