Question

【题目】如图，点A(2，2 ),N(1，0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.

Answer 1

【答案】
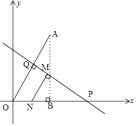
【解析】如图，过点A作AB⊥x轴，

则OB=2、AB=2 ，

∴OA= ，

∵cos∠AOB= ，

∴∠AOB=60°，

作AO的中垂线交x轴于点P，交OA于点Q，

则OQ=AQ=2，

∴OP= =4，

∵N(1,0)，

∴PN=3，

∵MO=MA，

∴点M在PQ上，

当MN⊥PQ时，MN最小，

∵PQ⊥OA、PQ⊥MN，

∴△PMN∽△PQO，

∴ ,即 ，

解得：MN= ，

故答案为： .

根据勾股定理求出OA的值，再根据三角函数得到∠AOB的度数，由MO=MA，得到点M在OA的垂直平分线上，得到△PMN∽△PQO，求出MN的值.