��Ŀ����
����Ŀ����1������̽����
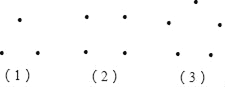
�����ÿ������Ի�һ��ֱ�ߣ���ô����������ͼ�зֱ��ߣ����ش����⣺
����1���������Ի�______��ֱ����
����2���������Ի�______��ֱ�ߣ�
����3���������Ի�______��ֱ�ߣ�
��2�����ɽ��ۣ�
���ƽ������n��n��3�����㣬��ÿ3���������һ��ֱ���ϣ���ô�����Ի���ֱ��______���������ú�n�Ĵ���ʽ��ʾ��
��3��������⣺
ij��50��ͬѧ�ڱ�ҵ���һ�ξۻ��У���ÿ������һ�����ʺã������� �����֣����ÿ������Ҫ����������������� �������
���𰸡���1����������2��![]() ��3��1225��2450
��3��1225��2450
��������
��1����������ȷ��һ��ֱ����ֱ�ߣ��۲�ɽ�����⣻
��2����������õ��Ĺ����ô���ʽ��ʾ���ɣ�
��3����n=50�����������ִ�����������ʱ��˫��ģ���������ִ�����2�����ɴ˼�����⣮
��1��ͼ�����£�
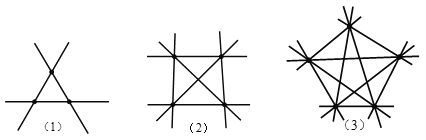
����ͼ�εã�
����1���������Ի�3��ֱ�ߣ�
����2���������Ի�6��ֱ�ߣ�
����3���������Ի�10��ֱ����
��2���ɣ�1����֪��
ƽ������3����ʱ�����ɻ�ֱ��1+2=3����
ƽ������4����ʱ�����ɻ�ֱ��1+2+3=6����
ƽ������5����ʱ�����ɻ�ֱ��1+2+3+4=10����
����
����ƽ������n��n��3�����㣬��ÿ3���������1��ֱ���ϣ���ô�����Ի�1+2+3+��+n-1=![]() ��ֱ����
��ֱ����
�ʴ�Ϊ��![]() ��
��
��3��ij��50��ͬѧ�ڱ�ҵ���һ�ξۻ��У���ÿ������1�����ʺã���ô����![]() =1225���֣�
=1225���֣�
����������1225��2=2450����
�ʴ�Ϊ��1225��2450.

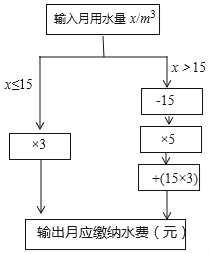
����Ŀ��С������������ˮ��˾�ľ�����ˮ�շѱ����ƶ���ˮ�Ѽ�����ֵת������ʾ��ͼ������ˮ����λ��m3��ˮ�ѵ�λ��Ԫ��
��1������ת��������������и�����Ӧ����ˮ��
�û� | �Ŵ�ү | ������ | С���� |
����ˮ��/m3 | 6 | 15 | 17 |
��Ӧ����ˮ��/Ԫ | �� �� | �� �� | �� �� |
��2����x��15ʱ���ú�x�Ĵ���ʽ��ʾˮ���� ����
��3��С����10�·�ˮ����70Ԫ��С����10�·���ˮ�� ��m3��