��Ŀ����
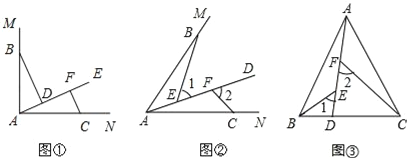
����Ŀ����ͼ����Rt��ABC�У���A��90��AB��6��AC��8��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE�����˶�������P��PQ��BC��Q������Q��QR��BA��AC��R������Q���C�غ�ʱ����Pֹͣ�˶�����BQ��x��QR��y��
��1�����D��BC�ľ���DH�ij���
��2����y����x�ĺ�����ϵʽ����Ҫ��д�Ա�����ȡֵ��Χ����
��3���Ƿ���ڵ�P��ʹ��PQRΪ���������Σ������ڣ��������������Ҫ���x��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��![]() ��2��
��2��![]() ��3������
��3������
��������
�����������1��������RQC�ס�ABC���������������εĶ�Ӧ�߳ɱ��������DH��
��2�����������ε����Ʊ����y����x�ĺ�����ϵʽ��
��3������ͼ�Σ�����ͼ�ν������ۣ�
�� ��PQ=PRʱ������P��PM��QR��M����QM=RM��������1+��2=90������C+��2=90�������1=��C��
��cos��1=cosC=![]() =
=![]() ����
����![]() ���������x��ֵ��
���������x��ֵ��
�� ��PQ=RQʱ��-![]() x+6=
x+6=![]() ��x=6��
��x=6��
����PR=QRʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬��CR=![]() CE=
CE=![]() AC=2��
AC=2��
�����������1��![]()
![]() ��AB=6��AC=8��
��AB=6��AC=8��![]() ��
��
![]() ��DΪAB�е㣬
��DΪAB�е㣬![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ,
,
��2��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ����
����![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ��
��
��3�����ڣ������������
����ͼ��1������![]() ʱ������P��
ʱ������P��![]() ��M����
��M����![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
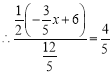 ��
��
![]() ��
��
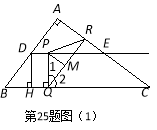
����ͼ��2������![]() ʱ��
ʱ��

![]() ��
��
![]() ��
��
����ͼ��3������![]() ʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬
ʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬
![]() ��
��
![]() ��
��
 ��
��
![]() ��
��
������������![]() Ϊ
Ϊ![]() ��6��
��6��![]() ʱ��
ʱ��![]() Ϊ���������Σ�
����������


 һ����������ϵ�д�
һ����������ϵ�д�����Ŀ����5�֣���2015����ɽ��ĩ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | 50 |
��1���뽫����������
��2���뽫����ͳ��ͼ����������
��3������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ��Ƕ��ٶȣ�