题目内容
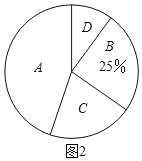
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,郑州市某校开设了“3D”打印、数学编程、智能机器人、陶艺制作”四门创客课程,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查(问卷调查表如表所示),将调查结果整理后绘制成图1、图2两幅均不完整的统计图表.
图1
创客课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
最受欢理的创客课程词查问卷
你好!这是一份关于你喜欢的创客深程问卷调查表,请你在表格中选择一个(只能选择一个)你最喜欢的课程选项在其后空格内打“√“,非常感谢你的合作.
选项 | 创客课程 | |
A | “3D”打印 | |
B | 数学编程 | |
C | 智能机器人 | |
D | 陶艺制作 |
请根据图表中提供的值息回答下列问题:
(1)统计表中的a= .b= ;
(2)“D”对应扇形的圆心角为 ;
(3)根据调查结果,请你估计该校2000名学生中最喜欢“数学编程”创客课程的人数.
【答案】(1)80,0.20;(2)36°;(3)500.
【解析】
(1)根据频数与频率的关系列式计算即可即可;
(2)根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;
(3)根据最喜欢“数学编程”创客课程的人数所占的百分比,即可得到人数.
解:(1)a=36÷0.45=80,
b=16÷80=0.20,
故答案为:80,0.20;
(2)“D”对应扇形的圆心角的度数为:![]() ×360°=36°,
×360°=36°,
故答案为:36°;
(3)估计该校2000名学生中最喜欢“数学编程”创客课程的人数为:2000×0.25=500(人).
故答案为:(1)80,0.20;(2)36°;(3)500.

 口算能手系列答案
口算能手系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
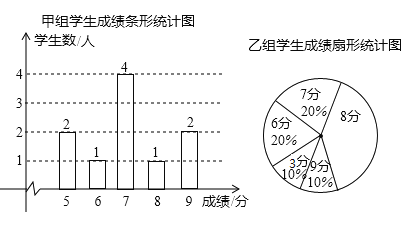
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.