题目内容
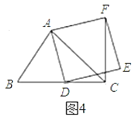
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一动点,连结
上一动点,连结![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() .
.
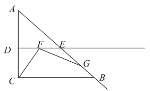
(1)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 的大小关系;
的大小关系;
(2)当![]() 等于多少时,
等于多少时,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)FG=FC(2) 6-3![]() 或3
或3![]() 或6+3
或6+3![]()
【解析】
(1)在DC上取一点M,使DM=DF,根据中位线和等腰直角三角形及线段的关系得到CM=EF,再判断出∠FCM=∠GFE,即可得出△EFG≌△MCF(ASA),即可求解;
(2)分点点F在DE上和DE的延长线上,构造直角三角形,建立方程求解即可得出结论.
(1)如图1,在DC上取一点M,使DM=DF,
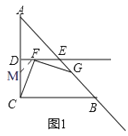
∵AC=BC,∠ACB=90![]() ,
,
∴∠A=∠ABC=45![]() ,
,
点D,E是AC,AB的中点,
∴DE=![]() BC=3,AD=CD=
BC=3,AD=CD=![]() AC=3,DE∥BC,
AC=3,DE∥BC,
∴CD=DE,∠ADE=∠CDE=∠ACB=90![]() ,∠AED=∠ABC=45
,∠AED=∠ABC=45![]()
∴CD-DM=DE-DF,
∴CM=EF,∠DMF=45![]() =∠AED,
=∠AED,
∴∠CMF=∠FEG,
∵CF⊥FG,
∴∠EFG+∠CFD=90![]() ,
,
∵∠DCF+∠CFD=90![]() ,
,
∴∠FCM=∠GFE,
在△EFG和△MCF中,

∴△EFG≌△MCF(ASA),
∴FG=FC;
(2)设DF=x,
∵AC=BC=6,
∴AB=![]()
∴BE=AE=![]() AB=3
AB=3![]()
①当点F在DE上时,如图2,

∵△BFG为等腰三角形,
∴FG=BG,
过点G作GN⊥DE于N,
∴∠FGN+∠GFN=90![]() ,
,
∵CF⊥FG
∴∠CFD+∠GFN=90![]() ,
,
∴∠CFD=∠FGN,
又CF=FG, ∠CDF=∠FNG=90![]()
∴△CDF≌△FNG,
∴FN=CD=3,
∴EN=DF=NG,
∴EG=![]() EN=
EN=![]() NG=
NG=![]() x,
x,
∴FG=BG=BE-EG=3![]() -
-![]() x,
x,
在Rt△FNG中,FG2NG2=FN2,
即:(3![]() -
-![]() x)2x2=9,
x)2x2=9,
∴x=6+3![]() (舍)或x=63
(舍)或x=63![]() ,
,
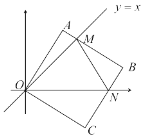
②当点F在DE的延长线上时,如图3

∵△BFG为等腰三角形,
Ⅰ、当BF=BG时,
过点B作BP⊥DE于P,
∴四边形BCDP是矩形,
∴BP=CD=3,DP=BC=6,
∴PF=DFDP=x6,
在图2中,FM=![]() DF=
DF=![]() x,
x,
∴EG=FM=![]() x,
x,
∴BF=BG=EGBE=![]() x3
x3![]() =
=![]() (x3),
(x3),
在Rt△BPF中,BF2PF2=BP2,
即:[![]() (x3)]2(x6)2=9.
(x3)]2(x6)2=9.
∴x=3![]() (舍)或x=3
(舍)或x=3![]() ,
,
Ⅱ、当BG=FG时,
BG=FG=CF=![]() ;EG=MF=
;EG=MF=![]() DF=
DF=![]() x;BE=3
x;BE=3![]()
∴![]() +3
+3![]() =
=![]() x,
x,
整理得:x212x+9=0
解得:x=6+3![]() 或x=63
或x=63![]() (不符题意舍去),
(不符题意舍去),
当BF=FG时,CF=FG=BF=![]() ,
,
∵CF=![]() ,
,
∴![]() =
=![]() ,
,
∴x=3(舍)
即:△BFG为等腰三角形时,x的值为6-3![]() 或3
或3![]() 或6+3
或6+3![]() .
.