题目内容
(6分)如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点。
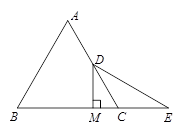

证明:连接BD,

∵在等边△ABC,且D是AC的中点,
∴∠DBC=1/2∠ABC=1/2×60°=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBC=∠E=30°,
∴BD=ED,△BDE为等腰三角形,
又∵DM⊥BC,
∴M是BE的中点。
分析:要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形的高和中线向重合即可得证。
解答:
证明:连接BD,

∵在等边△ABC,且D是AC的中点,
∴∠DBC=1/2∠ABC=1/2×60°=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBC=∠E=30°,
∴BD=ED,△BDE为等腰三角形,
又∵DM⊥BC,
∴M是BE的中点。
点评:本题考查了等腰三角形顶角平分线、底边上的中线和高三线合一的性质以及等边三角形每个内角为60°的知识.辅助线的作出是正确解答本题的关键。

练习册系列答案
相关题目
 都在方格纸的格点上,若
都在方格纸的格点上,若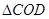 是由
是由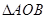 绕点
绕点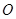 逆时针方向旋转而得,则旋转的角度为()
逆时针方向旋转而得,则旋转的角度为()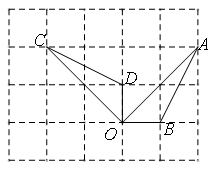




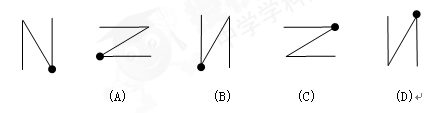

 的坐标为
的坐标为 ,
, 为坐标原点,连结
为坐标原点,连结 ,将线段
,将线段 ,则点
,则点 的坐标为 .
的坐标为 .