题目内容
【题目】在△ABC中,AB=AC. 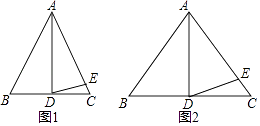
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= .
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= .
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?并给予证明.
【答案】
(1)15°
(2)20°
(3)解:∠BAD=2∠EDC(或∠EDC= ![]() ∠BAD);理由如下:
∠BAD);理由如下:
∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE
【解析】解:(1)∵在△ABC中,AB=AC,AD是BC上的高, ∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°;(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°;
所以答案是:15°;20°.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).

练习册系列答案
相关题目
【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?