题目内容
【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
(1)【回忆】
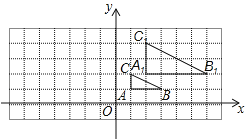
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.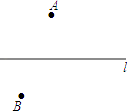
(2)【探索】
如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.
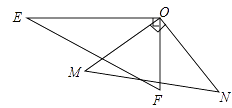
(3)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.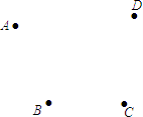
【答案】
(1)解:如图所示:
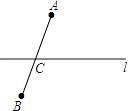
理由:两点之间线段最短;
(2)解:如图所示:
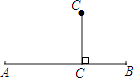
理由:点到直线的距离垂线段最短;
(3)解:如图所示:
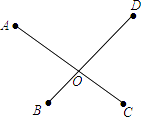
理由:两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上).
【解析】(1)根据两点之间线段最短,连接A,B交l于点C,点C就是所求的点;
(2)根据点到直线的距离垂线段最短,过点C作CO![]() AB于点O,点O就是所求的点;
AB于点O,点O就是所求的点;
(3)根据两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上)连接AC,BD两线相交于点O,点O就是所求得点。
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记,以及对点到直线的距离的理解,了解从直线外一点到这条直线的垂线段的长度叫做点到直线的距离.

练习册系列答案
相关题目