题目内容
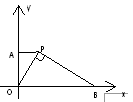
| 如图,已知P为正比例函数图象上一点,PA⊥y轴,垂足为A,PB⊥OP,与x轴交于点B。 (1)你能得出OP2=PA·OB的结论吗?说说你的理由。 (2)若P点的横坐标为1,B点的横坐标为5,求 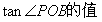 。 。(3)求经过点P和点B的直线解析式。 |
 |
| (1) 能得到结论。 因为∠AOP与∠PBD都是∠POB的余角 所以 ∠AOP=∠PBO 又 ∠PAO= ∠OPB=90° 所以 △POA∽△OPB 所以 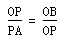 即 OP2 =PA·OB ; (2)设点P的坐标为(1,m)则点A(0,m)、B(5,0) 因为 PC2 =PA·BD=1×5 所以 PO = 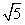 又 PB2 =OB2-PO2= 52-( 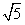 )2=20 )2=20 所以 PB =2 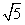 所以 所以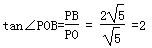 ; ;(3)作PD⊥x 轴 ,垂足为D,则 OP2=OD2+PD2=1+m2 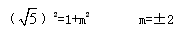 所以 m = 2 点P的坐标为(1,2) 设直线PB的解析式为 y = kx+b 则有  解得 解得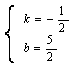 所以 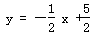 |
 |

练习册系列答案
相关题目
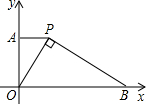 如图,已知P为正比例函数图象上一点,PA⊥y轴,垂足为A,PB⊥OP,与x轴交于点B.
如图,已知P为正比例函数图象上一点,PA⊥y轴,垂足为A,PB⊥OP,与x轴交于点B. ,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.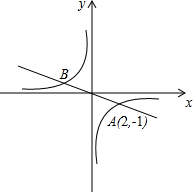 如图,已知反比例函数
如图,已知反比例函数 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.