题目内容
【题目】如图,在Rt△ABC中∠C=90°,放置边长分别为4,6,x的三个正方形,则x的值为 ( )
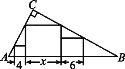
A. 24 B. 12 C. 10 D. 8
【答案】C
【解析】
根据已知条件可以推出△OME∽△PFN然后把它们的直角边用含x的表达式表示出来,利用对应边的比相等,即可推出x的值.
∵∠PFN+∠CFE=90°, ∠CEF+∠CFE=90°,
∴∠PFN=∠CEF.
∵∠EMO+∠MEO=90°, ∠CEF+∠MEO=90°,
∴∠EMO=∠CEF,
∴∠EMO=∠PFN.
又∵∠MOE=∠FPN=90°,
∴△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=4,PN=6,
∴OE=x-4,PF=x-6,
∴(x-4):6=4:(x-6),
∴(x-4)(x-6)=24,
∴x=0(不符合题意,舍去),x=10.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目