题目内容
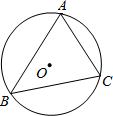 (2012•河东区一模)如图,已知△ABC的外接圆O的半径为
(2012•河东区一模)如图,已知△ABC的外接圆O的半径为| 2 |
45°
45°
.分析:首先连接OA,OC,由勾股定理的逆定理,即可证得∠AOC=90°,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得答案.
解答: 解:连接OA,OC,
解:连接OA,OC,
∵△ABC的外接圆O的半径为
,AC=2,
∴OA2+OB2=4=AC2,
∴∠AOC=90°,
∴∠ABC=
∠AOC=45°.
故答案为:45°.
 解:连接OA,OC,
解:连接OA,OC,∵△ABC的外接圆O的半径为
| 2 |
∴OA2+OB2=4=AC2,
∴∠AOC=90°,
∴∠ABC=
| 1 |
| 2 |
故答案为:45°.
点评:此题考查了圆周角定理与勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
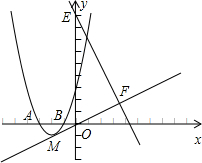 (Ⅰ)求抛物线C的解析式;
(Ⅰ)求抛物线C的解析式;