题目内容
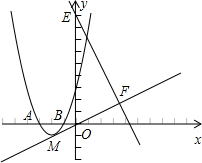
(2012•河东区一模)如图,抛物线C:y=ax2+bx+3与x轴的两个交点坐标为A(-3,0),B(-1,0).
 (Ⅰ)求抛物线C的解析式;
(Ⅰ)求抛物线C的解析式;
(Ⅱ)设抛物线C的顶点为M,直线y=-2x+9与y轴交于点E,交直线OM于点F.现保持抛物线C的形状和开口方向,使顶点沿直线OM移动(O为坐标原点).在平移过程中,当抛物线与射线EF(含端点E、F)只有一个公共点时,求它的顶点横坐标的值或取值范围;
(Ⅲ)将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于M,N两点.问在y轴的负半轴上是否存在点P,使△PMN的内心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
 (Ⅰ)求抛物线C的解析式;
(Ⅰ)求抛物线C的解析式;(Ⅱ)设抛物线C的顶点为M,直线y=-2x+9与y轴交于点E,交直线OM于点F.现保持抛物线C的形状和开口方向,使顶点沿直线OM移动(O为坐标原点).在平移过程中,当抛物线与射线EF(含端点E、F)只有一个公共点时,求它的顶点横坐标的值或取值范围;
(Ⅲ)将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于M,N两点.问在y轴的负半轴上是否存在点P,使△PMN的内心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(Ⅰ)将A(-3,0)、B(-1,0),代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(Ⅱ)配方后即可确定其顶点坐标,然后利用平移规律确定函数的解析式,然后根据射线与抛物线有唯一的公共点求得h的值或取值范围即可;
(Ⅲ)将抛物线平移,当顶点至原点时,其解析式为y=x2,设MN的解析式为y=kx+3(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.根据△PMN的内心在y轴上,得到∠GMP=∠MPQ=∠QPN=∠HNP,从而△GMP∽△HNP,利用相似三角形对应边成比例即可列出有关t的方程求解即可.
(Ⅱ)配方后即可确定其顶点坐标,然后利用平移规律确定函数的解析式,然后根据射线与抛物线有唯一的公共点求得h的值或取值范围即可;
(Ⅲ)将抛物线平移,当顶点至原点时,其解析式为y=x2,设MN的解析式为y=kx+3(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.根据△PMN的内心在y轴上,得到∠GMP=∠MPQ=∠QPN=∠HNP,从而△GMP∽△HNP,利用相似三角形对应边成比例即可列出有关t的方程求解即可.
解答:解:(Ⅰ)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点
∴9a-3b+3=0且a-b+3=0
解得a=1,b=4
∴抛物线的解析式为y=x2+4x+3
(Ⅱ)由(Ⅰ)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,-1)
∴直线OM的解析式为y=
x
于是设平移的抛物线的顶点坐标为(h,
h),
∴平移的抛物线解析式为y=(x-h)2+
h,.
①当抛物线经过点E时,
∵E(0,9),
∴h2+
h=9,
解得h=
.
∴当
≤h<
时,
平移的抛物线与射线EF只有一个公共点.
②当抛物线与射线EF只有一个公共点时,
由方程组y=(x-h)2+
h,y=-2x+9.
得 x2+(-2h+2)x+h2+
h-9=0,
∴△=(-2h+2)2-4(h2+
h-9)=0,
解得h=4.
此时抛物线y=(x-4)2+2与射线EF唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与射线EF只有一个公共点时,
顶点横坐标的值或取值范围是 h=4或
≤h<
.
(Ⅲ)将抛物线平移,当顶点至原点时,其解析式为y=x2,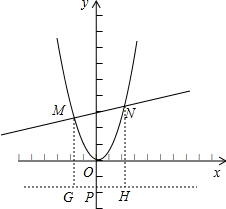
设MN的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.
∵△PMN的内心在y轴上,
∴∠GMP=∠MPQ=∠QPN=∠HNP,
∴△GMP∽△HNP,
∴
=
,
∴
=
=
∴2kxE•xF=(t-3)(xE+xF)
由y=x2,y=kx+3.得x2-kx-3=0.
∴xE+xF=k,xE•xF=-3.
∴2k(-3)=(t-3)k,
∵k≠0,
∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使△PMN的内心在y轴上.
∴9a-3b+3=0且a-b+3=0
解得a=1,b=4
∴抛物线的解析式为y=x2+4x+3
(Ⅱ)由(Ⅰ)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,-1)
∴直线OM的解析式为y=
| 1 |
| 2 |
于是设平移的抛物线的顶点坐标为(h,
| 1 |
| 2 |
∴平移的抛物线解析式为y=(x-h)2+
| 1 |
| 2 |
①当抛物线经过点E时,
∵E(0,9),
∴h2+
| 1 |
| 2 |
解得h=
-1±
| ||
| 4 |
∴当
-1-
| ||
| 4 |
-1+
| ||
| 4 |
平移的抛物线与射线EF只有一个公共点.
②当抛物线与射线EF只有一个公共点时,
由方程组y=(x-h)2+
| 1 |
| 2 |
得 x2+(-2h+2)x+h2+
| 1 |
| 2 |
∴△=(-2h+2)2-4(h2+
| 1 |
| 2 |
解得h=4.
此时抛物线y=(x-4)2+2与射线EF唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与射线EF只有一个公共点时,
顶点横坐标的值或取值范围是 h=4或
-1-
| ||
| 4 |
-1+
| ||
| 4 |
(Ⅲ)将抛物线平移,当顶点至原点时,其解析式为y=x2,

设MN的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.
∵△PMN的内心在y轴上,
∴∠GMP=∠MPQ=∠QPN=∠HNP,
∴△GMP∽△HNP,
∴
| GP |
| PH |
| GM |
| HN |
∴
| -xE |
| xF |
| yE-t |
| yF-t |
| kxE+3-t |
| kxF+3-t |
∴2kxE•xF=(t-3)(xE+xF)
由y=x2,y=kx+3.得x2-kx-3=0.
∴xE+xF=k,xE•xF=-3.
∴2k(-3)=(t-3)k,
∵k≠0,
∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使△PMN的内心在y轴上.
点评:此题主要考查了二次函数的综合应用以及相似三角形的应用,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.

练习册系列答案
相关题目