题目内容
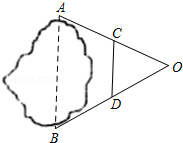
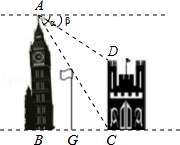
如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,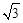 ≈1.732)
≈1.732)

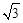 ≈1.732)
≈1.732)
解:设EC=x米,
在Rt△BCE中,∠EBC=30°,∴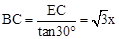 。
。
在Rt△BCD中,∠DBC=60°,∴CD=BC•tan60°=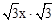 =3x。
=3x。
在Rt△ACD中,∠DBC=45°,∴AC=CD,即: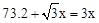 。
。
解得: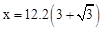 。
。
∴塔高DE=CD﹣EC=3x﹣x=2x=2×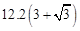 =
=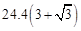 ≈115.5(米)。
≈115.5(米)。
答:塔高DE约为115.5米。
在Rt△BCE中,∠EBC=30°,∴
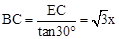 。
。在Rt△BCD中,∠DBC=60°,∴CD=BC•tan60°=
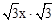 =3x。
=3x。在Rt△ACD中,∠DBC=45°,∴AC=CD,即:
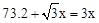 。
。解得:
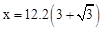 。
。∴塔高DE=CD﹣EC=3x﹣x=2x=2×
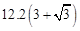 =
=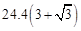 ≈115.5(米)。
≈115.5(米)。答:塔高DE约为115.5米。
试题分析:设EC=x,则在Rt△BCE中,BC=
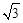 EC=
EC=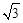 x;在Rt△BCD中,CD=
x;在Rt△BCD中,CD=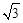 BC=3x;在Rt△ACD中,AC=AB+BC=73.2+
BC=3x;在Rt△ACD中,AC=AB+BC=73.2+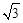 x,CD=3x,利用关系式AC=CD列方程求出x,从而塔高DE=CD﹣EC=2x可以求出。
x,CD=3x,利用关系式AC=CD列方程求出x,从而塔高DE=CD﹣EC=2x可以求出。 
练习册系列答案
相关题目
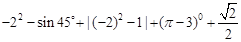 ;
;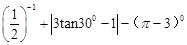 ;
;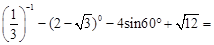 .
.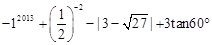
 ≈1.4,
≈1.4, ≈1.7)
≈1.7)
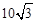 米
米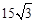 米
米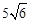 米
米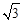 ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: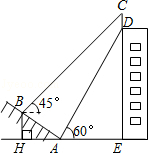
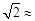 1.414,
1.414,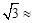 1.732)
1.732)