题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
【答案】![]()
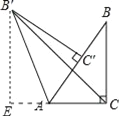
【解析】试题分析:作B′E⊥AC交CA的延长线于E,首先求出AC的长度,根据旋转图形的性质求出AE的长度,然后根据RtAB′E的勾股定理求出B′E的长度,最后根据Rt△CEB′的勾股定理得出答案.
试题解析:如图,作B′E⊥AC交CA的延长线于E, ∵∠ACB=90°,∠BAC=60°,AB=2, ∴∠ABC=30°, ∴AC=![]() AB=1,
AB=1,
∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,
∴AB=AB′=2,∠B′AB=60°, ∴∠EAB′=180°﹣∠B′AB﹣∠BAC=60°, ∵B′E⊥EC, ∴∠AB′E=30°,
∴AE=1, 在Rt△AB′E中,∵AE=1,AB′=2, ∴B′E=![]() =
=![]() , ∴EC=AE+AC=2,
, ∴EC=AE+AC=2,
在Rt△CEB′中,∵B′E=![]() ,CE=2, ∴B′C=
,CE=2, ∴B′C=![]() =
=![]() .
.

练习册系列答案
相关题目