题目内容
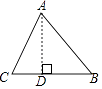
【题目】如图，点P是等边△ABC内一点，连接PA，PB，PC，PA：PB：PC=3：4：5，以AC为边作△AP′C≌△APB，连接PP′，则有以下结论：①△APP′是等边三角形；②△PCP′是直角三角形；③∠APB=150°；④∠APC=105°．其中一定正确的是 ． （把所有正确答案的序号都填在横线上） 
【答案】①②③
【解析】解：△ABC是等边三角形，则∠BAC=60°，又△AP'C≌△APB，则AP=AP′，∠PAP′=∠BAC=60°， ∴△APP'是正三角形，①正确；
又PA：PB：PC=3：4：5，
∴设PA=3x，则：PP′=PA=3x，P′C=PB=4x，PC=5x，
根据勾股定理的逆定理可知：△PCP'是直角三角形，且∠PP′C=90°，②正确；
又△APP'是正三角形，
∴∠AP′P=60°，
∴∠APB=150°③正确；错误的结论只能是∠APC=105°．
所以答案是①②③．
【考点精析】掌握全等三角形的性质和勾股定理的逆定理是解答本题的根本，需要知道全等三角形的对应边相等; 全等三角形的对应角相等；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
通城学典默写能手系列答案
相关题目
