题目内容
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.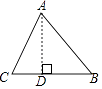
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
【答案】
(1)14﹣x
(2)解:∵AD⊥BC,
∴AD2=AC2﹣CD2,AD2=AB2﹣BD2,
∴132﹣(14﹣x)2=152﹣x2,
解得:x=9
(3)解:由(2)得:AD= ![]() =
= ![]() =12,
=12,
∴S△ABC= ![]() BCAD=
BCAD= ![]() ×14×12=84
×14×12=84
【解析】解:(1)∵BC=14,BD=x, ∴DC=14﹣x,
所以答案是:14﹣x;
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目