题目内容
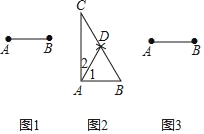
【题目】如图，点 A，C 是数轴上的点，点 A 在原点上，AC=10．动点 P，Q 网时分别从 A，C 出发沿数轴正方向运动，速度分别为每秒 3 个单位长度和每秒 1 个单位长度，点 M 是 AP 的中点，点 N 是 CQ 的中点．设运动时间为t秒(t>0)
(1) 点C表示的数是______ ；点P表示的数是______，点Q表示的数是________（点P．点 Q 表示的数用含 t 的式子表示)
(2) 求 MN 的长；
(3) 求 t 为何值时，点P与点Q相距7个单位长度？
【答案】（1）
（2）
（3）
或
【解析】
（1）根据动点P、Q的运动轨迹可得
，
，即可解答．
（2）根据中点平分线段长度和线段的和差关系即可解答．
（3）由（1）可得
，代入求解即可．
（1）∵点 A，C 是数轴上的点，点 A 在原点上，AC=10
∴点C表示的数是10
∵动点 P，Q 网时分别从 A，C 出发沿数轴正方向运动，速度分别为每秒 3 个单位长度和每秒 1 个单位长度
∴，
∴点P表示的数是
，点Q表示的数是
故答案为：．
（2）∵点 M 是 AP 的中点，点 N 是 CQ 的中点，，
∴
，
∴
．
（3）∵点P表示的数是，点Q表示的数是
∴
∵点P与点Q相距7个单位长度
∴
解得
或
．
【题目】某厂按用户的月需求量x（件）完成一种产品的生产，其中x＞0，每件的售价为18万元，每件的成本y（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x（件）成反比，经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12），符合关系式x=2n2﹣2kn+9（k+3）（k为常数），且得到了表中的数据．
月份n（月） | 1 | 2 |
成本y（万元/件） | 11 | 12 |
需求量x（件/月） | 120 | 100 |
（1）求y与x满足的关系式，请说明一件产品的利润能否是12万元；
（2）求k，并推断是否存在某个月既无盈利也不亏损；
（3）在这一年12个月中，若第m个月和第（m+1）个月的利润相差最大，求m．
