题目内容
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).
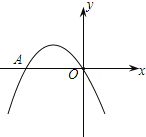
(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
【答案】(1)二次函数的解析式为y=﹣x2﹣4x;(2)点P的坐标是:(﹣2,4)、(﹣2+2![]() ,﹣4)、(﹣2﹣2
,﹣4)、(﹣2﹣2![]() ,﹣4).
,﹣4).
【解析】
试题分析:(1)把点A原点的坐标代入函数解析式,利用待定系数法求二次函数解析式解答;
(2)根据三角形的面积公式求出点P到AO的距离,然后分点P在x轴的上方与下方两种情况解答即可.
解:(1)由已知条件得![]() ,
,
解得![]() ,
,
所以,此二次函数的解析式为y=﹣x2﹣4x;
(2)∵点A的坐标为(﹣4,0),
∴AO=4,
设点P到x轴的距离为h,
则S△AOP=![]() ×4h=8,
×4h=8,
解得h=4,
①当点P在x轴上方时,﹣x2﹣4x=4,
解得x=﹣2,
所以,点P的坐标为(﹣2,4),
②当点P在x轴下方时,﹣x2﹣4x=﹣4,
解得x1=﹣2+2![]() ,x2=﹣2﹣2
,x2=﹣2﹣2![]() ,
,
所以,点P的坐标为(﹣2+2![]() ,﹣4)或(﹣2﹣2
,﹣4)或(﹣2﹣2![]() ,﹣4),
,﹣4),
综上所述,点P的坐标是:(﹣2,4)、(﹣2+2![]() ,﹣4)、(﹣2﹣2
,﹣4)、(﹣2﹣2![]() ,﹣4).
,﹣4).

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目