Question

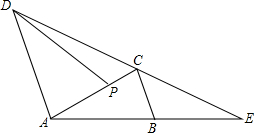
已知：如图，在△ABC中，AB=AC=4，BC=

1

2

AB，P是边AC上的一个点，AP=

1

2

PD，∠APD=∠ABC，连接DC并延长交边AB的延长线于点E．
（1）求证：AD∥BC；
（2）设AP=x，BE=y，求y关于x的函数解析式，并写出它的定义域；
（3）连接BP，当△CDP与△CBE相似时，试判断BP与DE的位置关系，并说明理由．

Answer 1

分析：（1）利用相似比相等证明△DAP∽△ABC，求得∠DAP=∠ACB，然后利用内错角相等，两直线平行，推出结论．
（2）设AP=x，则AD=2x．由已知BC=

1

2

AB，AB=4，得出BC=2．利用AD∥BC，从而得出

y

y+4

=

2

2x

，整理，得y关于x的函数解析式为y=

4

x-1

．
（3）由图形得知，当△CDP与△CBE相似时，∠PCD=∠BCE，推出

BE

BC

=

DP

PC

，即

y

2

=

2x

4-x

，求得x、y的值，从而得出BP∥DE．

解答：解：
（1）证明：∵BC=

1

2

AB，AP=

1

2

PD，∴

BC

AB

=

AP

PD

．
（1分）
又∵∠APD=∠ABC，∴△APD∽△ABC．（1分）
∴∠DAP=∠ACB，（1分）
∴AD∥BC．（1分）

（2）解：∵AB=AC，∴∠ABC=∠ACB．
∴∠DAP=∠DPA，
∴AD=PD．（1分）
∵AP=x，∴AD=2x．（1分）
∵BC=

1

2

AB，AB=4，∴BC=2．
∵AD∥BC，∴

BE

AE

=

BC

AD

，即

y

y+4

=

2

2x

．（1分）
整理，得y关于x的函数解析式为y=

4

x-1

．（1分）
定义域为1＜x≤4．（1分）

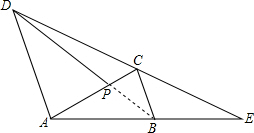
（3）解：平行．（1分）
证明：∵∠CPD=∠CBE，∠PCD＞∠E，
∴当△CDP与△CBE相似时，∠PCD=∠BCE．（1分）
∴

BE

BC

=

DP

PC

，即

y

2

=

2x

4-x

．（1分）
把y=

4

x-1

代入，整理得x²=4．
∴x=2，x=-2（舍去）．（1分）
∴y=4，
∴AP=CP，AB=BE，（1分）
∴BP∥CE，即BP∥DE．

点评：本题主要考查了相似三角形的判定和性质，二次函数以及平行线的判定等知识点，综合性强．