题目内容
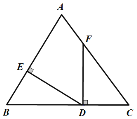
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
【答案】55°
【解析】
由图示知:∠FDC+∠AFD=180°,则∠FCD=55°.通过全等三角形Rt△BDE≌△Rt△CFD(HL)的对应角相等推知∠BDE=∠CFD.
如图,∵∠FDC+∠FCD=∠AFD=145°,
∴∠FCD=55°.
∴∠CFD=35°
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,![]() ,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∵∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.

练习册系列答案
相关题目