题目内容
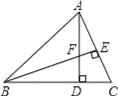
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.

(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
【答案】(1)证明见试题解析;(2)4.5.
【解析】
试题分析:(1)利用D是BC边上的中点,DE⊥BC可以得到∠EBC=∠ECB,而由AD=AC可以得到∠ADC=∠ACD,再利用相似三角形的判定,就可以证明题目结论;
(2)过点A作AM⊥BC,垂足是M,利用等腰三角形性质求出DM,利用平行线性质定理,求出AM,从而求出△ABC的面积,再利用相似三角形的性质就可以求出三角形FCD的面积.
试题解析:(1)∵D是BC边上的中点,DE⊥BC,∴BD=DC,∠EDB=∠EDC=90°,∴△BDE≌△EDC,∴∠B=∠DCE,∵AD=AC,∴∠ADC=∠ACB,∴△ABC∽△FCD;
(2)过点A作AM⊥BC,垂足是M,∵△ABC∽△FCD,BC=2CD,∴![]() ,
,![]() ,
,
∵DE⊥BC,∴D是BC边上的中点,∴BD=DC,∵BC=8,∴DC=4,∵AD=AC,AM⊥DC,∴DM=MC=2,∴BM=4+2=6,
∵DE⊥BC,AM⊥DC,∴DE∥AM,∴![]() ,∴
,∴![]() ,
,![]() ,,∴S△ABC=
,,∴S△ABC=![]() BC×AM=
BC×AM=![]() ,∵
,∵![]() ,∴
,∴![]() .
.


练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目