题目内容
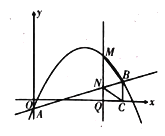
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 、
、![]() 分别落在点
分别落在点![]() 、
、![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去……,若点
轴上,依次进行下去……,若点![]() ,
,![]() .则点
.则点![]() 的坐标是( )
的坐标是( )
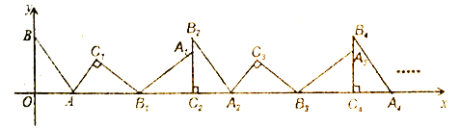
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差6个单位长度,根据这个规律可以求得B2019的坐标.
解:
∵A(![]() ,B(0,2),
,B(0,2),
∴Rt△AOB中,AB=![]() ,
,
∴OA+AB1+B1C2=![]() =6
=6
∴B2的横坐标为6,且B2C2=2,即B2(6,2),
∴B4的横坐标为;2![]() =12,
=12,
∴点B2018的横坐标为:2018÷2×6=6054,纵坐标为:2,即B2018的坐标是(6054,2),
∴点B2019的横坐标为6054+![]() =6058,
=6058,
∴点B2019的坐标为(6058,0).
故选C.

 阅读快车系列答案
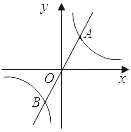
阅读快车系列答案【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.
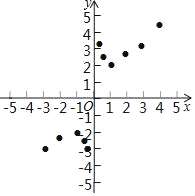
【题目】赣县田村素称“灯彩之乡”,田村花灯源于唐代,盛于宋朝,迄今已有1300多年历史了,某公司生产了一种田村花灯,每件田村花灯制造成本为20元.设销售单价x(元),每日销售量y(件)、每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
销售单价x(元) | 30 | 31 | 32 | 40 |
销售量y(件) | 40 | 38 | 36 | 20 |
(1)根据表中数据的规律、分別写出每日销售量y(件)、每日利润w(元)关于销售单价x(元)之间的函数表达式(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?