ЬтФПФкШн
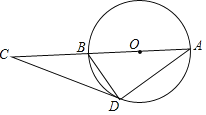
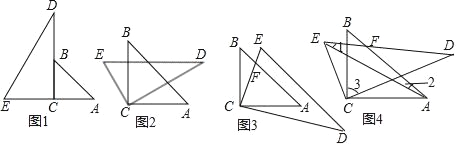
ЁОЬтФПЁПНЋСНПщШ§НЧАхАДЭМ1АкЗХЃЌЙЬЖЈШ§НЧАхABCЃЌНЋШ§НЧАхCDEШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЌЦфжаЁЯAЃН45ЁуЃЌЁЯDЃН30ЁуЃЌЩша§зЊНЧЮЊІСЃЌЃЈ0ЁуЃМaЃМ80ЁуЃЉ
ЃЈ1ЃЉЕБDEЁЮACЪБЃЈШчЭМ2ЃЉЃЌЧѓІСЕФжЕЃЛ
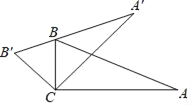
ЃЈ2ЃЉЕБDEЁЮABЪБЃЈШчЭМ3ЃЉЃЎABгыCEЯрНЛгкЕуFЃЌЧѓІСЕФжЕЃЛ
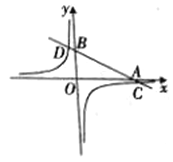
ЃЈ3ЃЉЕБ0ЁуЃМІСЃМ90ЁуЪБЃЌСЌНсAEЃЈШчЭМ4ЃЉЃЌжБЯпABгыDEЯрНЛгкЕуFЃЌЪдЬНОПЁЯ1+ЁЯ2+ЁЯ3ЕФДѓаЁЪЧЗёИФБфЃПШєВЛИФБфЃЌЧыЧѓГіДЫЖЈжЕЃЌШєИФБфЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЛ
ЃЈ2ЃЉ105ЁуЃЛ
ЃЈ3ЃЉВЛБфЃЌЦфжЕЮЊ105ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩDEЁЮACПЩЕУЁЯDCAЃНЁЯDЃН30ЁуЃЌдђПЩЧѓЁЯІСЃНЁЯDCBЃН60ЁуЃЛ
ЃЈ2ЃЉгЩDEЁЮABПЩЕУЁЯEЃНЁЯAFCЃН60ЁуЃЌИљОнШ§НЧаЮФкНЧКЭПЩЧѓЁЯFCAЃН75ЁуМДПЩЧѓЁЯACDЃН15ЁуЃЌдђПЩЧѓЁЯІСЃЛ
ЃЈ3ЃЉИљОнШ§НЧаЮФкНЧКЭКЭЭтНЧЕШгкВЛЯрСкЕФСНИіФкНЧКЭЃЌСаГіЁЯ1ЃЌЁЯ2ЃЌЁЯ3ЙиЯЕЪНПЩЧѓЁЯ1+ЁЯ2+ЁЯ3ЕФжЕ.
ЃЈ1ЃЉЁпDEЁЮACЃЌ
ЁрЁЯDЃНЁЯACDЃН30ЁуЃЌ
гжЁпЁЯBCAЃН90ЁуЃЌ
ЁрЁЯBCDЃНЁЯBCAЉЁЯACDЃН60ЁуЃЌМДІСЃН60ЁуЃЛ
ЃЈ2ЃЉЁпDEЁЮABЃЌ
ЁрЁЯEЃНЁЯCFAЃН60ЁуЃЌ
гжЁпЁЯCFAЃНЁЯB+ЁЯBCEЃЌ
ЁрЁЯBCEЃН15ЁуЃЌ
ЁрЁЯBCDЃНЁЯECD+ЁЯBCEЃН105ЁуЃЌМДІСЃН105ЁуЃЛ
ЃЈ3ЃЉДѓаЁВЛБфЃЌЦфжЕЮЊ105ЁуЃЌ
ЁпЁЯACD+ЁЯCABЃНЁЯD+ЁЯAFDЃЌЁЯCABЃН45ЁуЃЌЁЯDЃН30ЁуЃЌ
ЁрЁЯAFDЉЁЯACDЃН15ЁуЃЌ
гжЁпЁЯ1+ЁЯ2ЃНЁЯAFDЃЌЁЯ3ЃН90ЁуЉЁЯACDЃЌ
ЁрЁЯ1+ЁЯ2+ЁЯ3ЃНЁЯAFD+90ЁуЉЁЯACDЃН90Ёу+15ЁуЃН105Ёу.

 ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИЁОЬтФПЁПаЁУїЙКТђAЃЌBСНжжЩЬЦЗЃЌУПДЮЙКТђЭЌвЛжжЩЬЦЗЕФЕЅМлЯрЭЌЃЌОпЬхаХЯЂШчЯТБэЃК
ДЮЪ§ | ЙКТђЪ§СПЃЈМў | ЙКТђзмЗбгУЃЈдЊ | |
A | B | ||
ЕквЛДЮ | 2 | 1 | 55 |
ЕкЖўДЮ | 1 | 3 | 65 |
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓAЃЌBСНжжЩЬЦЗЕФЕЅМлЃЛ
ЃЈ2ЃЉШєЕкШ§ДЮЙКТђетСНжжЩЬЦЗЙВ12МўЃЌЧвAжжЩЬЦЗЕФЪ§СПВЛЩйгкBжжЩЬЦЗЪ§СПЕФ2БЖЃЌЧыЩшМЦГізюЪЁЧЎЕФЙКТђЗНАИЃЌВЂЫЕУїРэгЩЃЎ
ЁОЬтФПЁППЦбЇМвЮЊСЫЭЦВтзюЪЪКЯФГжжефЦцжВЮяЩњГЄЕФЮТЖШЃЌНЋетжжжВЮяЗжБ№ЗХдкВЛЭЌЮТЖШЕФЛЗОГжаЃЌОЙ§вЛЖЈЪБМфКѓЃЌВтЪдГіетжжжВЮяИпЖШЕФдіГЄЧщПіЃЌВПЗжЪ§ОнШчЯТБэЃК
ЮТЖШt/Ёц | Ё | Љ5 | Љ3 | 2 | Ё |
жВЮяИпЖШдіГЄСПh/mm | Ё | 34 | 46 | 41 | Ё |
ПЦбЇМвЭЦВтГіhЃЈmmЃЉгыtжЎМфЕФЙиЯЕПЩвдНќЫЦЕигУЖўДЮКЏЪ§РДПЬЛЃЎвбжЊЮТЖШдНЪЪКЯЃЌжВЮяИпЖШдіГЄСПдНДѓЃЌгЩДЫПЩвдЭЦВтзюЪЪКЯетжжжВЮяЩњГЄЕФЮТЖШЮЊЃЈЁЁЁЁЃЉ
A. Љ2Ёц B. Љ1Ёц C. 0Ёц D. 1Ёц