题目内容
(如图,已知∠AOB=ll0°,∠AOC=m∠AOD,∠COE=n∠BOC,且3(m-2)+4=m+2,单项式 的系数为n.
的系数为n.
(1)求4(m-n) 2-(m-n) 2-5的值;
(2)当∠COD:∠COE=3:2时,试求∠COD的度数.
 的系数为n.
的系数为n.(1)求4(m-n) 2-(m-n) 2-5的值;
(2)当∠COD:∠COE=3:2时,试求∠COD的度数.
(1) ;(2)33°
;(2)33°
 ;(2)33°
;(2)33°试题分析:(1)先解方程3(m-2)+4=m+2得到m的值,再根据单项式的系数的定义得到n的值,然后化简代数式,最后代入求值;
(2)由(1)可知∠AOC =2∠AOD,∠COE=
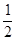 ∠BOC,则可得∠AOD=
∠BOC,则可得∠AOD=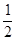 ∠AOC,∠COD=∠AOC-∠AOD=
∠AOC,∠COD=∠AOC-∠AOD=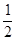 ∠AOC,从而求得∠COD+∠COE=55°,设∠COD=3x°,则∠COE=2x°,即可列方程求解.
∠AOC,从而求得∠COD+∠COE=55°,设∠COD=3x°,则∠COE=2x°,即可列方程求解.(1)解方程3(m-2)+4=m+2得m="2"
由已知有n=
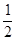
∴4(m-n)2-(m-n)2-5=3(m-n)2-5
当m=2,n=
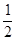 时,m-n=
时,m-n= ,原式=3×(
,原式=3×( )2-5=
)2-5=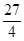 -5=
-5= ;
;(2)由(1)可知:∠AOC =2∠AOD,∠COE=
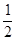 ∠BOC
∠BOC∴∠AOD=
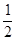 ∠AOC,∠COD=∠AOC-∠AOD=
∠AOC,∠COD=∠AOC-∠AOD=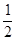 ∠AOC
∠AOC ∴∠COD+∠COE=
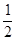 (∠AOC+∠BOC)=
(∠AOC+∠BOC)=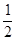 ∠AOB=55°
∠AOB=55°设∠COD=3x°,则∠COE=2x°
∴3x+2x=55
∴x=11
∴∠COD=33°.
点评:本题知识点较多,综合性强,难度较大,需要学生熟练掌握各方面的基础知识.

练习册系列答案
相关题目


 个工人,生产特种螺栓和螺帽,一个螺栓的两头各套上一个螺帽配成一套,每人每天平均生产螺栓
个工人,生产特种螺栓和螺帽,一个螺栓的两头各套上一个螺帽配成一套,每人每天平均生产螺栓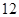 个或螺帽
个或螺帽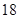 个.设
个.设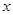 个工人生产螺栓,要使一天所生产的螺栓和螺帽刚好配套,那么可列出方程 .
个工人生产螺栓,要使一天所生产的螺栓和螺帽刚好配套,那么可列出方程 .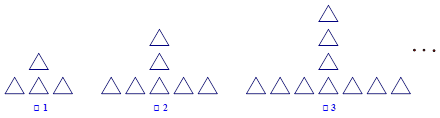
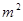 ,面积如图所示(单位:米,卫生间的宽未定,设宽为
,面积如图所示(单位:米,卫生间的宽未定,设宽为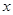 米),售房部为张先生提供了以下两种优惠方案
米),售房部为张先生提供了以下两种优惠方案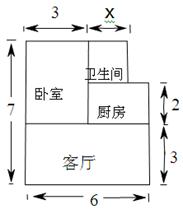
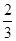 的面积;
的面积;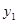 表示方案一中购买一套该户型商品房的总金额,用
表示方案一中购买一套该户型商品房的总金额,用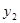 表示方案二中购买一套该户型商品房的总金额,分别求出
表示方案二中购买一套该户型商品房的总金额,分别求出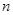 (
(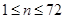 ,
,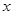 的方程
的方程 是一元一次方程,则
是一元一次方程,则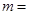 .
.