题目内容
我们知道,对于二次函数y=a(x+m)2+k的图象,可由函数y=ax2的图象进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”.左右、上下平移的路径称为朋友路径,对应点之间的线段距离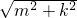 称为朋友距离.
称为朋友距离.
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”.
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”.
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离= .
.
(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向______,再向下平移7单位,相应的朋友距离为______.
(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离.
(3)探究三:为函数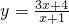 和它的基本函数
和它的基本函数 ,找到朋友路径,并求相应的朋友距离.
,找到朋友路径,并求相应的朋友距离.
解:(1)y=2(x+1)-7,
∴向左平移1个单位;
朋友距离为 =5
=5 ;
;
(2)基本函数为y=x2;
∵原抛物线的顶点坐标为(0,0),新抛物线的顶点坐标为(3,-4),
∴朋友路径为先向右平移3个单位,再向下平移4个单位;
相应的朋友距离 =5;
=5;
(3)函数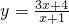 可化为y=
可化为y= +3,
+3,
∴朋友路径为先向左平移1个单位,再向上平移3个单位.相应的朋友距离为 =
= .
.
分析:(1)把y=2x-5换一种方法拆分,保证最后的常数项为-7,朋友距离等于两次移动距离的平方和的算术平方根;
(2)基本函数只包括二次项的系数,并且二次项的系数不变;找到新抛物线的顶点坐标即可求得朋友路径,朋友距离等于两次移动距离的平方和的算术平方根;
(3)把所给函数进行拆分,同理得到朋友路径与距离.
点评:解决本题的关键是理解所给范例中的朋友函数和朋友距离的概念,并结合其余函数的特点在其余函数中加以运用.
∴向左平移1个单位;
朋友距离为
 =5
=5 ;
;(2)基本函数为y=x2;
∵原抛物线的顶点坐标为(0,0),新抛物线的顶点坐标为(3,-4),
∴朋友路径为先向右平移3个单位,再向下平移4个单位;
相应的朋友距离
 =5;
=5;(3)函数
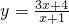 可化为y=
可化为y= +3,
+3,∴朋友路径为先向左平移1个单位,再向上平移3个单位.相应的朋友距离为
 =
= .
.分析:(1)把y=2x-5换一种方法拆分,保证最后的常数项为-7,朋友距离等于两次移动距离的平方和的算术平方根;
(2)基本函数只包括二次项的系数,并且二次项的系数不变;找到新抛物线的顶点坐标即可求得朋友路径,朋友距离等于两次移动距离的平方和的算术平方根;
(3)把所给函数进行拆分,同理得到朋友路径与距离.
点评:解决本题的关键是理解所给范例中的朋友函数和朋友距离的概念,并结合其余函数的特点在其余函数中加以运用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 称为朋友距离。
称为朋友距离。 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。 .
. 和它的基本函数
和它的基本函数 ,找到朋友路径,
,找到朋友路径, 称为朋友距离。
称为朋友距离。 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。 .
. 和它的基本函数
和它的基本函数 ,找到朋友路径,
,找到朋友路径, 称为朋友距离。
称为朋友距离。 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。 .
. 和它的基本函数
和它的基本函数 ,找到朋友路径,
,找到朋友路径,