题目内容
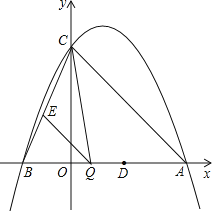
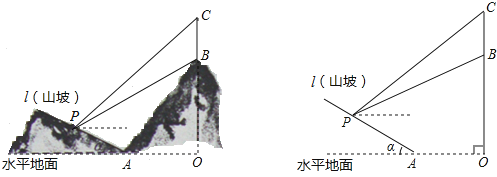
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)
【答案】解:如图,过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形.
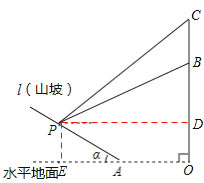
在Rt△PBD中,∵∠BDP=90°,∠BPD=26.6°,
∴BD=PDtan∠BPD=PDtan26.6°。
在Rt△CBD中,∵∠CDP=90°,∠CPD=37°,
∴CD=PDtan∠CPD=PDtan37°。
∵CD﹣BD=BC,∴PDtan37°﹣PDtan26.6°=80。
∴0.75PD﹣0.50PD=80,解得PD=320。
∴BD=PDtan26.6°≈320×0.50=160。
∵OB=220,∴PE=OD=OB﹣BD=60。
∵OE=PD=320,∴AE=OE﹣OA=320﹣200=120。
∴![]() 。∴α≈26.6°。
。∴α≈26.6°。
【解析】
试题过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形,先解Rt△PBD,得出BD=PDtan26.6°;解Rt△CBD,得出CD=PDtan37°;再根据CD﹣BD=BC,列出方程,求出PD=320,进而求出PE=60,AE=120,然后在△APE中利用三角函数的定义即可求解。

练习册系列答案
相关题目