题目内容
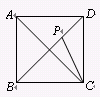
已知:如图,四边形ABCD是平行四边形,△ADE和△BCF都是等边三角形.求证:BD和EF互相平分. 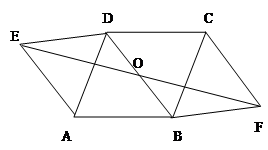

见解析
连接BE、DF,根据平行四边形的性质得∠1=∠2.再根据,△ADE和△BCF都是等边三角形,得出DEBF平行且相等,根据平行四边形的性质推出结论.
解:连接BE、DF.

∵
 , ∴
, ∴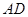 ∥
∥ ,
,
∵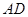 ∥,
∥, ∴∠1=∠2.
∴∠1=∠2.
∵等边三角形 ,∴
,∴ ,∠3=60°,
,∠3=60°,
∵等边三角形 ,∴
,∴ ,∠4=60°,
,∠4=60°,
∴ ,
,
∠1+∠3=∠2+∠4,即∠ ∠
∠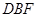 ,∴
,∴ ∥
∥ ,
,
∴四边形 是平行四边形
是平行四边形
∴BD和EF互相平分
解:连接BE、DF.

∵

 , ∴
, ∴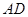 ∥
∥ ,
,∵
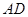 ∥,
∥, ∴∠1=∠2.
∴∠1=∠2. ∵等边三角形
 ,∴
,∴ ,∠3=60°,
,∠3=60°, ∵等边三角形
 ,∴
,∴ ,∠4=60°,
,∠4=60°, ∴
 ,
,∠1+∠3=∠2+∠4,即∠
 ∠
∠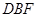 ,∴
,∴ ∥
∥ ,
,∴四边形
 是平行四边形
是平行四边形∴BD和EF互相平分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

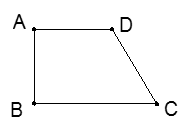

 ,以A为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是 .
,以A为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是 .
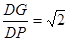 ;
; .其中正确的是
.其中正确的是