题目内容
【题目】已知:如图,把![]() 向上平移
向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到
个单位长度,得到![]() ;
;
(1)写出![]() 的坐标;
的坐标;
(2)求出![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
【答案】(1)A′(0,4)、B′(-1,1)、C′(3,1);(2)6;(3)P(0,1)或(0,-5).
【解析】
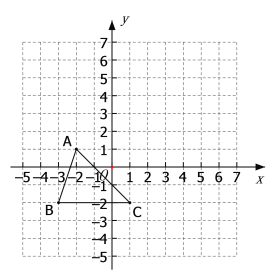
(1)观察图形可得△ABC的各顶点坐标,继而根据上加下减,左减右加即可得到平移后对应点A′、B′、C′的坐标;即可得到△A′B′C′;
(2)直接利用三角形面积公式根据BC以及BC边上的高进行求解即可;
(3)由△BCP与△ABC的面积相等可知点P到BC的距离等于点A到BC的距离,据此分情况求解即可.
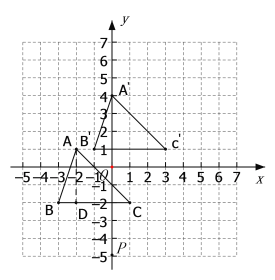
(1)观察图形可得A(-2,1),B(-3,-2),C(1,-2),
因为把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′,
所以A′(-2+2,1+3)、B′(-3+2,-2+3)、C′(1+2,-2+3),
即A′(0,4)、B′(-1,1)、C′(3,1);
(2)S△ABC=![]() =
=![]() =6;
=6;
(3)设P(0,y),
∵△BCP与△ABC同底等高,
∴|y+2|=3,即y+2=3或y+2=-3,解得y1=1,y2=-5,
∴P(0,1)或(0,-5).

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目