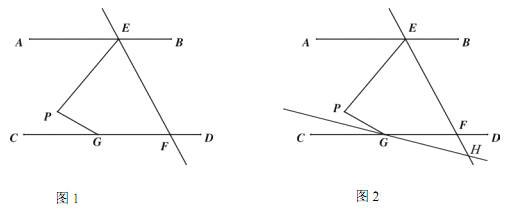题目内容
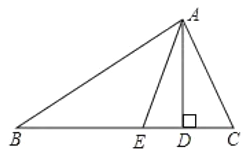
【题目】如图(1),点B、C、E在同一直线上![]() .
.
(1)求证:![]() ;
;

(2)若![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,请直接写出图(2)中所有与
,请直接写出图(2)中所有与![]() 互余的角.
互余的角.

【答案】(1)见解析;(2)∠ABF、∠ACB、∠D、∠GEC
【解析】
(1)利用三角形外角的性质即可得出结论;
(2)利用BF⊥AC可得∠A与∠ABF互余,根据∠ABC=90°可得∠A与∠ACB互余,再结合∠A=∠DCE可得∠A与∠D互余,最后结合GE⊥CD可得∠A与∠GEC互余.
解:(1)∵![]() ,
,
∠ACE=∠B+∠BAC,
∴∠BAC=∠DCE;
(2)∵BF⊥AC,
∴∠A+∠ABF=90°,
∵∠ABC=90°,
∴∠ACB+∠A=90°,
∵∠A=∠DCE,∠DEC=90°,
∴∠DCE+∠D=90°,
即∠A+∠D=90°,
∵GE⊥CD,
∴∠GCE+∠GEC=90°,
∴∠GEC+∠A=90°,
故与∠A互余的角有:∠ABF、∠ACB、∠D、∠GEC.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目