题目内容
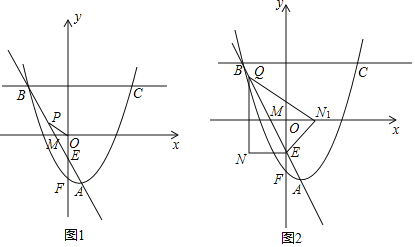
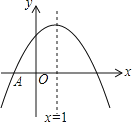
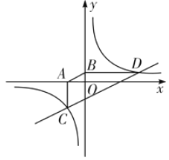
【题目】已知直线![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(Ⅰ)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(Ⅱ)试探究直线![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(Ⅲ)已知点![]() ,且
,且![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,若当
上,若当![]() (其中
(其中![]() )时,函数
)时,函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)若![]() ,则
,则 ,
,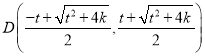 ,若
,若![]() ,则
,则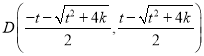 ,
,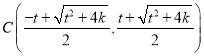 ;(Ⅱ)
;(Ⅱ)![]() ,理由见解析;(Ⅲ)
,理由见解析;(Ⅲ)![]() 的值为
的值为![]()
【解析】
(Ⅰ)把直线y=x+t与双曲线![]() 的解析式联立成方程组,解方程组即可求出交点坐标,即C、D两点的坐标;
的解析式联立成方程组,解方程组即可求出交点坐标,即C、D两点的坐标;
(Ⅱ)位置关系是:平行,求出直线AB的解析式,与直线CD的解析式y=x+t比较,k相等说明两直线平行;
(Ⅲ)先求出C点坐标,再利用待定系数法求出抛物线的解析式,最后通过分类讨论:①当![]() 时,②当
时,②当![]() ,③当
,③当![]() ,分别根据函数
,分别根据函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,结合二次函数的性质列出方程,得出m,n的值.
,结合二次函数的性质列出方程,得出m,n的值.
解:(Ⅰ)联立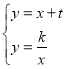 ,解得:
,解得: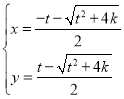 或
或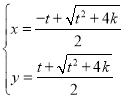 ,
,
设![]() ,
,![]() ,
,
若![]() ,则
,则 ,
,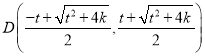 ,
,
若![]() ,则
,则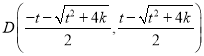 ,
,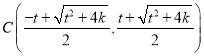 ;
;
(Ⅱ)![]() ,
,
理由:不妨设![]() ,
,
由(1)知 ,
, 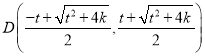 ,
,
∴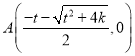 ,
, ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则将![]() ,
,![]() 两点坐标代入有:
两点坐标代入有:![]() ,
,![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∴直线![]() 与
与![]() 的位置关系是
的位置关系是![]() ;
;
(Ⅲ)将![]() 代入双曲线
代入双曲线![]()
![]() 得
得![]() ,
,
将![]() 代入直线
代入直线![]() ,得
,得![]() ,
,
∵![]() ,
,
∴由(Ⅰ)知 ,
,
∴![]() ,
,
∵![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
即![]() ,
,
由![]() ,可知
,可知![]() ,
,![]() ,
,
①当![]() 时,由函数的最小值为
时,由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知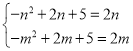 ,
,
∴![]() ,
,![]() 即为一元二次方程
即为一元二次方程![]() 的两解,即
的两解,即![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴此情况不合题意;
②当![]() ,即
,即![]() 时,
时,
由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知![]() ,
,
解得: ,
,
此时![]() ,即
,即![]() ,符合题意,
,符合题意,
∴![]() ;
;
③当![]() ,即
,即![]() 时,
时,
由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴此情况不合题意,
综上所述,满足题意的![]() 的值为
的值为![]() .
.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.