题目内容
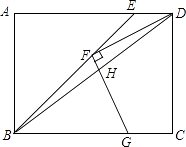
【题目】如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )

A. 若AE=CE,则DE=FE B. 若DE=FE,则AE=CE
C. 若BC=CF,则AD=CF D. 若AD=CF,则DE=FE
【答案】C
【解析】由题目已知条件、结合每个选项分别证得三角形全等即可判断得出答案.
∵AB∥FC,
∴∠A=∠ACF,∠ADE=∠F,
当AE=CE时,利用AAS则可证得△ADE≌△CFE,则有DE=EF,故A选项说法是正确的,不符合题意,
当DE=FE时,同理可证得△ADE≌△CFE,则有AE=CE,故B选项说法是正确的,不符合题意,
当BC=CF时,无法证明△ADE≌△CFE,即无法得出AD=CF,故C说法是错误的,符合题意,
当AD=CF时,利用ASA则可证得△ADE≌△CFE,则有DE=FE,故D选项是正确的,不符合题意,
故选:C.

练习册系列答案
相关题目