题目内容
如图，已知二次函数y＝ax2＋bx＋c的图象交x轴的负半轴于点A（－5，0），交y轴于点B，过点B作BC⊥y轴交函数y＝ax2＋bx＋c的图象于点C（－2，4）．
（1）设函数y＝ax2＋bx＋c的图象与x轴的另一个交点为D，求△ABD的面积．
（2）若P为y轴上的一个动点，连接PA、PC，分别过A、C作PC、PA的平行线交于点Q，连接PQ．试探究：
①是否存在这样的点P，使得PQ2＝PA2＋PC2？为什么？
②是否存在这样的点P，使
得PQ取得最小值？若存在，请求出这个最小值
，并求出此时点P的坐标；若不存在，请说明理由．
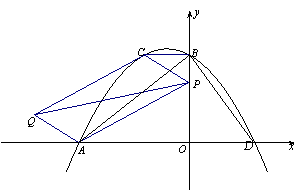
②连接AC交PQ于点M，如右图所示．∵四边形PAQC为平行四边形，∴M为AC、PQ的中点．………（8分）PQ取得最小值时，MP必定取得最小值．
显然，当P为OB的中点时，由梯形中位线定理可得MO∥CB，∴MP⊥y轴．此时MP取得最小值，为
×(2＋5)＝
．∴PQ的最小值为7．…………（9分） PQ取得最小值时，P（0，2）．……（10分）
练习册系列答案
阅读快车系列答案
相关题目
三角形与△BOF相似？若存在，请求出P点的坐标；若不存在，请说明理由．
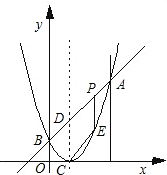如图，已知二次函数图象的顶点坐标为C（1，0），直线y=x+b与该二次函数的图象交于A、B两点，其中点A的坐标为（3，4），点B在y轴上．点P为线段AB上的一个动点（点P与A、B不重合），过点P作x轴的垂线与该二次函数的图象交于点E．
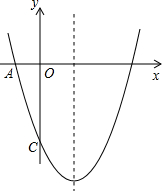如图，已知二次函数y=ax2-4x+c的图象与坐标轴交于点A（-1，0）和点C（0，-5）．
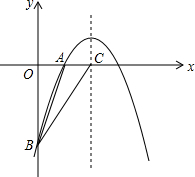（2012•衡水一模）如图，已知二次函数