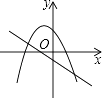题目内容
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A、B,AB=2,与y轴交于点C,对称轴为直线x=2,对称轴交x轴于点M.
(1)求抛物线的函数解析式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,则点D的坐标为 .
【答案】
(1)
解:抛物线与x轴交于点A、B,且AB=2,
根据对称性,得AM=MB=1,
∵对称轴为直线x=2,
∴OA=1,OB=3,
∴点A、B的坐标分别为(1,0)、(3,0),
把A、B两点坐标代入y=x2+bx+c,得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为:y=x2﹣4x+3
(2)
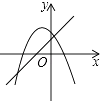
解:如图1中,连结BC,与对称轴交点则为点P,连接AP、AC.
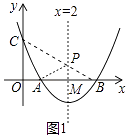
由线段垂直平分线性质,得AP=BP,
∴CB=BP+CP=AP+CP,
∴AC+AP+CP=AC+BC,
根据“两点之间,线段最短”,得△APC周长的最小,
∵C为(0,3)
∴OC=3,
在Rt△AOC中,有AC= ![]() =
= ![]() ,
,
在Rt△BOC中,有BC= ![]() =3
=3 ![]() ,
,
∴△APC的周长的最小值为: ![]() +3
+3 ![]()
(3)(2,﹣1)
【解析】解: (3)如图2中,当点D为抛物线的顶点时,EM=DM时,以点A、B、D、E为顶点的四边形是菱形,此时点D(2,﹣1)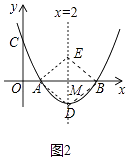
所以答案是D(2,﹣1).
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

 名校通行证有效作业系列答案
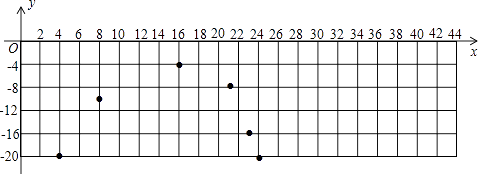
名校通行证有效作业系列答案【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至﹣20℃时,制冷再次停止,…,按照以上方式循环进行. 同学们记录了44min内15个时间点冷柜中的温度y(℃)随时间x(min)的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数. ①当4≤x<20时,写出一个符合表中数据的函数解析式;
②当20≤x<24时,写出一个符合表中数据的函数解析式;
(2)a的值为;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当4≤x≤44时温度y随时间x变化的函数图象.