题目内容
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
| x (元) | 15 | 20 | 25 | … |
| y (件) | 25 | 20 | 15 | … |
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
解:(1)设此一次函数解析式为y=kx+b(k,b为常数,且k≠0).
则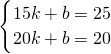 .
.
解得k=-1,b=40
即一次函数解析式为y=-x+40
(2)当x=30时,每日的销售量为y=-30+40=10(件)
每日所获销售利润为(30-10)×10=200(元)
分析:(1)已知日销售量y是销售价x的一次函数,可设函数关系式为y=kx+b(k,b为常数,且k≠0),代入两组对应值求k、b,确定函数关系式.
(2)把x=30代入函数式求y,根据:(售价-进价)×销售量=利润,求解.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题.
则
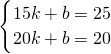 .
.解得k=-1,b=40
即一次函数解析式为y=-x+40
(2)当x=30时,每日的销售量为y=-30+40=10(件)
每日所获销售利润为(30-10)×10=200(元)
分析:(1)已知日销售量y是销售价x的一次函数,可设函数关系式为y=kx+b(k,b为常数,且k≠0),代入两组对应值求k、b,确定函数关系式.
(2)把x=30代入函数式求y,根据:(售价-进价)×销售量=利润,求解.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元?
| x(元) | 15 | 20 | 30 | … |
| y(件) | 25 | 20 | 10 | … |
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元?
某产品每件成本10元,在试销阶段每件产品的日销售价x(元)与产品的日销售量y(件)之间的关系如下表:
(1)在草稿纸上描点,观察点的分布,确定y与x的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
| x(元) | 15 | 20 | 25 | … |
| y(件) | 25 | 20 | 15 | … |
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
| x (元) | 15 | 20 | 25 | … |
| y (件) | 25 | 20 | 15 | … |
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
某产品每件成本10元,试销阶段每件产品的日销售价x(元)与产品的日销售量y(件)之间的关系如下表:
(1)请在直角坐标系上描点,观察点的分布,建立y与x的恰当函数模型.
(2)若要求每天卖出24件,则这一天它能获利多少元?
| x(元) | 15 | 20 | 25 | 30 | … |
| y(件) | 25 | 20 | 15 | 10 | … |
(2)若要求每天卖出24件,则这一天它能获利多少元?