题目内容
某产品每件成本10元，试销阶段每件产品的日销售价x（元）与产品的日销售量y（件）之间的关系如下表：| x（元） | 15 | 20 | 25 | 30 | … |
| y（件） | 25 | 20 | 15 | 10 | … |
（2）若要求每天卖出24件，则这一天它能获利多少元？
分析：（1）根据表格数据知价格每涨5元销售量就少5件，初步判断为一次函数，再根据所描点的情形作出判断，最后验证；
（2）一天的利润=单价的利润×销售量．
（2）一天的利润=单价的利润×销售量．
解答：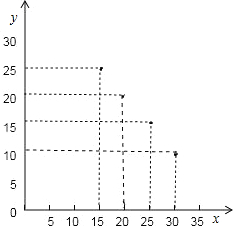
解：（1）根据所描点的情形，判断为一次函数．
设解析式为y=kx+b，根据图象过点（20，20）、（30，10），
得
，解得
，
所以解析式为y=-x+40．
分别把其余两点的坐标代入关系式验证，判断成立．
（2）设日利润为w，则w=y（x-10），
=（-x+40）（x-10），
=-x2+50x-400，
=-（x-25）2+225，
当x=24时，w=-（24-25）2+225=224，即每天卖出25件，能获利224元．
解：（1）根据所描点的情形，判断为一次函数．设解析式为y=kx+b，根据图象过点（20，20）、（30，10），
得
|
|
所以解析式为y=-x+40．
分别把其余两点的坐标代入关系式验证，判断成立．
（2）设日利润为w，则w=y（x-10），
=（-x+40）（x-10），
=-x2+50x-400，
=-（x-25）2+225，
当x=24时，w=-（24-25）2+225=224，即每天卖出25件，能获利224元．
点评：根据图表判断函数类型时，先作出初步判断，求出关系式后再验证．
练习册系列答案
轻松暑假总复习系列答案
相关题目
某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：
若日销售量y是销售价x的一次函数．
（1）求出日销售量y（件）是销售价x（元）的函数关系式；
（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日的销售利润是多少元？
| x（元） | 15 | 20 | 30 | … |
| y（件） | 25 | 20 | 10 | … |
（1）求出日销售量y（件）是销售价x（元）的函数关系式；
（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日的销售利润是多少元？
某产品每件成本10元，在试销阶段每件产品的日销售价x（元）与产品的日销售量y（件）之间的关系如下表：
（1）在草稿纸上描点，观察点的分布，确定y与x的函数关系式；
（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？
| x（元） | 15 | 20 | 25 | … |
| y（件） | 25 | 20 | 15 | … |
（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？
某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：
若日销售量y是销售价x的一次函数．
（1）求出日销售量y（件）与销售价x（元）的函数关系式；
（2）求销售价定为30元时，每日的销售利润．
| x （元） | 15 | 20 | 25 | … |
| y （件） | 25 | 20 | 15 | … |
（1）求出日销售量y（件）与销售价x（元）的函数关系式；
（2）求销售价定为30元时，每日的销售利润．