题目内容
【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: ![]() ≈1.41).
≈1.41).
【答案】解:作EF⊥AC,
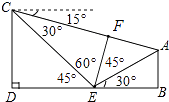
根据题意,CE=18×15=270米,
∵tan∠CED=1,
∴∠CED=∠DCE=45°,
∵∠ECF=90°-45°-15°=30°,
∴EF= ![]() CE=135米,
CE=135米,
∵∠CEF=60°,∠AEB=30°,
∴∠AEF=180°-45°-60°-30°=45°,
∴AE=135 ![]()
∴AB= ![]() ×135
×135 ![]() ≈95.2米.
≈95.2米.
【解析】先根据路程的公式求出CE的长,作EF⊥AC,再根据直角三角形中,30°角所对的直角边等于斜边的一半,求出EF的长,再在△AEF中,利用解直角三角形求出AE的长,然后再根据直角三角形的性质求出AB的长。
【考点精析】关于本题考查的含30度角的直角三角形和特殊角的三角函数值,需要了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能得出正确答案.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目