题目内容
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=______度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.
【答案】(1)900;(2)①α+β=180°;②当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
【解析】
(1)问要求∠BCE的度数,可将它转化成与已知角有关的联系,根据已知条件和全等三角形的判定定理,得出△ABD≌△ACE,再根据全等三角形中对应角相等,最后根据直角三角形的性质可得出结论;(2)问在第(1)问的基础上,将α+β转化成三角形的内角和;(3)问是第(1)问和第(2)问的拓展和延伸,要注意分析两种情况.
(1)90°.
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,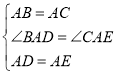
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
又∵∠BAC=90°
∴∠BCE=90°;
(2)①α+β=180°,
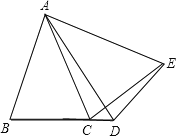
理由:∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
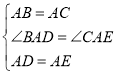
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②当点D在射线BC上时,α+β=180°;
理由:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵在△ABD和△ACE中
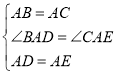
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠BAC+∠ABD+∠BCA=180°,
∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,
∴α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
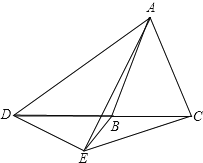
理由:∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
∵在△ADB和△AEC中,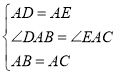
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE,
∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,
∴∠BAC=∠BCE,
即α=β.