题目内容
(2012•哈尔滨)已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.
(1)如图1,求证:PC=AN;
(2)如图2,点E是MN上一点,连接EP并延长交BC于点K,点D是AB上一点,连接DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,PC=3,CK:CF=2:3,求DQ的长.
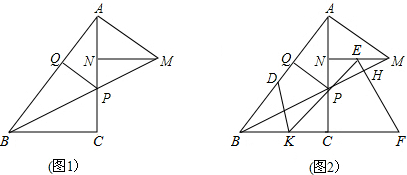
(1)如图1,求证:PC=AN;
(2)如图2,点E是MN上一点,连接EP并延长交BC于点K,点D是AB上一点,连接DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,PC=3,CK:CF=2:3,求DQ的长.

分析:(1)要点是确定一对全等三角形△AQP≌△MNA,得到AN=PQ;然后推出BP为角平分线,利用角平分线的性质得到PC=PQ;从而得到PC=AN;
(2)要点是按照已知条件,求出线段KC的长度,从而确定△PKC是等腰直角三角形;然后在△BDK中,解直角三角形即可求得BD、DQ的长度.
(2)要点是按照已知条件,求出线段KC的长度,从而确定△PKC是等腰直角三角形;然后在△BDK中,解直角三角形即可求得BD、DQ的长度.
解答:(1)证明:证法一:
如图①,∵BA⊥AM,MN⊥AC,
∴∠BAM=ANM=90°,
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,
∴∠PAQ=∠AMN,
∵PQ⊥AB MN⊥AC,
∴∠PQA=∠ANM=90°,
∴AQ=MN,
∴△AQP≌△MNA(ASA)
∵AN=PQ AM=AP,
∴∠AMB=∠APM
∵∠APM=∠BPC,∠BPC+∠PBC=90°,∠AMB+∠ABM=90°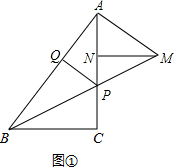
∴∠ABM=∠PBC
∵PQ⊥AB,PC⊥BC
∴PQ=PC(角平分线的性质),
∴PC=AN;
证法二:
如图①,∵BA⊥AM,MN⊥AC,
∴∠BAM=ANM=90°
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°
∴∠PAQ=∠AMN
∵PQ⊥AB,
∴∠AQP=90°=∠ANM
∵AQ=MN,
∴△PQA≌△ANM(ASA)
∴AP=AM,PQ=AN,
∴∠APM=∠AMP
∵∠AQP+∠BAM=180°,
∴PQ∥MA
∴∠QPB=∠AMP
∵∠APM=∠BPC,
∴∠QPB=∠BPC
∵∠BQP=∠BCP=90°,BP=BP
∴△BPQ≌△BPC(AAS)
∴PQ=PC,
∴PC=AN.
(2)解:解法一: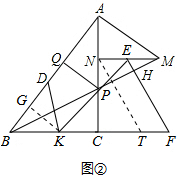
如图②,∵NP=2 PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5 AC=8,
∴AM=AP=5
∴AQ=MN=
=4
∵∠PAQ=∠AMN∠ACB=∠ANM=90°
∴∠ABC=∠MAN
∴tan∠ABC=tan∠MAN=
=
∵tan∠ABC=
,
∴BC=6
∵NE∥KC,
∴∠PEN=∠PKC,
又∵∠ENP=∠KCP
∴△PNE∽△PCK,
∴
=
,
∵CK:CF=2:3,
设CK=2k,则CF=3k
∴
=
,NE=
k.
过N作NT∥EF交CF于T,则四边形NTFE是平行四边形
∴NE=TF=
k,
∴CT=CF-TF=3k-
k=
k
∵EF⊥PM,
∴∠BFH+∠HBF=90°=∠BPC+∠HBF,
∴∠BPC=∠BFH
∵EF∥NT,
∴∠NTC=∠BFH=∠BPC
tan∠NTC=tan∠BPC=
=2,
∴tan∠NTC=
=2,
∴CT=
k=
,
∴k=
,
∴CK=2×
=3,BK=BC-CK=3
∵∠PKC+∠DKB=∠ABC+∠BDK,∠DKE=∠ABC,
∴∠BDK=∠PKC,
tan∠PKC=
=1,
∴tan∠BDK=1.
过K作KG⊥BD于G
∵tan∠BDK=1,tan∠ABC=
,
∴设GK=4n,则BG=3n,GD=4n
∴BK=5n=3,
∴n=
,
∴BD=4n+3n=7n=
∵AB=
=10,AQ=4,
∴BQ=AB-AQ=6
∴DQ=BQ-BD=6-
=
.
解法二: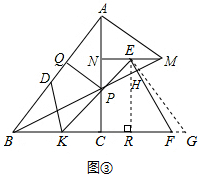
如图③,∵NP=2,PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5,AC=8,
∴AM=AP=5
∴AQ=MN=
=4
∵NM∥BC,
∴∠NMP=∠PBC
又∵∠MNP=∠BCP,
∴△MNP∽△BCP
∴
=
,
∴
=
BC=6
作ER⊥CF于R,则四边形NERC是矩形
∴ER=NC=5,NE=CR
∵∠BHE=∠BCR=90°
∴∠EFR=90°-∠HBF∠BPC=90°-∠HBF
∴∠EFR=∠BPC,
∴tan∠EFR=tan∠BPC,
∴
=
,即
=
∴RF=
,
∵NE∥KC,
∴∠NEP=∠PKC
又∵∠ENP=∠KCP,
∴△NEP∽△CKP,
∴
=
=
∵CK:CF=2:3,设CK=2k,CF=3k
∴NE=CR=
k,CR=CF-RF=3k-
,
∴3k-
=
k
∴k=
,
∴CK=3 CR=2
∴BK=3
在CF的延长线上取点G,使∠EGR=∠ABC,
∴tan∠EGR=tan∠ABC
∴
=
=
,
∴RG=
ER=
,EG=
=
,KG=KC+CR+RG=
,
∵∠DKE+∠EKC=∠ABC+∠BDK,∠ABC=∠DKE,
∴∠BDK=∠EKC,
∴△BDK∽△GKE,
∴
=
∴BD•EG=BK•KG,
∴∠BDK=∠EKC,
∴△BDK∽△GKE,
∴BD=
∵AB=
=10,AQ=4,
∴BQ=AB-AQ=6
∴DQ=BQ-BD=6-
=
解法三: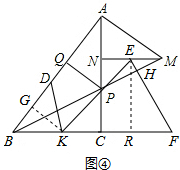
如图④,∵NP=2,PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5,AC=8,
∴AM=AP=5
∴AQ=MN=
=4
∵NM∥BC,
∴∠EMH=∠PBC∠PEN=∠PKC
又∵∠PNE=∠PCK,
∴△PNE∽△PCK,△PNM∽△PCB
∴
=
,
=
,
∵CK:CF=2:3,
设CK=2k,CF=3k
∴
=
,
=
,
∴NE=
k,BC=6
∴BF=6+3k,ME=MN-NE=4-
k
tan∠ABC=
=
,BP=
=3
∴sin∠EMH=sin∠PBC=
=
∵EF⊥PM,
∴FH=BFsin∠PBC=
(6+3k)
EH=EMsin∠EMH=
(4-
k)
∴tan∠REF=tan∠PBC=
,
∵tan∠REF=
∴RF=
∴EF=
=
,
∵EH+FH=EF
∴
(4-
k)+
(6+3k)=
,
∴k=
∴CK=2×
=3,BK=BC-CK=3
∵∠PKC+∠DKE=∠ABC+∠BDK∠DKE=∠ABC,
∴∠BDK=∠PKC
∵tan∠PKC=1,
∴tan∠BDK=1,
过K作KG⊥BD于G
∵tan∠BDK=1,tan∠ABC=
∴设GK=4n,则BG=3n,GD=4n
∴BK=5n=3,
∴n=
,
∴BD=4n+3n=7n=
∵AB=
=10,AQ=4,
∴BQ=AB-AQ=6,
∴DQ=BQ-BD=6-
=
.
如图①,∵BA⊥AM,MN⊥AC,
∴∠BAM=ANM=90°,
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,
∴∠PAQ=∠AMN,
∵PQ⊥AB MN⊥AC,
∴∠PQA=∠ANM=90°,
∴AQ=MN,
∴△AQP≌△MNA(ASA)
∵AN=PQ AM=AP,
∴∠AMB=∠APM
∵∠APM=∠BPC,∠BPC+∠PBC=90°,∠AMB+∠ABM=90°

∴∠ABM=∠PBC
∵PQ⊥AB,PC⊥BC
∴PQ=PC(角平分线的性质),
∴PC=AN;
证法二:
如图①,∵BA⊥AM,MN⊥AC,
∴∠BAM=ANM=90°
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°
∴∠PAQ=∠AMN
∵PQ⊥AB,
∴∠AQP=90°=∠ANM
∵AQ=MN,
∴△PQA≌△ANM(ASA)
∴AP=AM,PQ=AN,
∴∠APM=∠AMP
∵∠AQP+∠BAM=180°,
∴PQ∥MA
∴∠QPB=∠AMP
∵∠APM=∠BPC,
∴∠QPB=∠BPC
∵∠BQP=∠BCP=90°,BP=BP
∴△BPQ≌△BPC(AAS)
∴PQ=PC,
∴PC=AN.
(2)解:解法一:

如图②,∵NP=2 PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5 AC=8,
∴AM=AP=5
∴AQ=MN=
| AM2-AN2 |
∵∠PAQ=∠AMN∠ACB=∠ANM=90°
∴∠ABC=∠MAN
∴tan∠ABC=tan∠MAN=
| MN |
| AN |
| 4 |
| 3 |
∵tan∠ABC=
| AC |
| BC |
∴BC=6
∵NE∥KC,
∴∠PEN=∠PKC,
又∵∠ENP=∠KCP
∴△PNE∽△PCK,
∴
| NE |
| CK |
| NP |
| PC |
∵CK:CF=2:3,
设CK=2k,则CF=3k
∴
| NE |
| 2k |
| 2 |
| 3 |
| 4 |
| 3 |
过N作NT∥EF交CF于T,则四边形NTFE是平行四边形
∴NE=TF=
| 4 |
| 3 |
∴CT=CF-TF=3k-
| 4 |
| 3 |
| 5 |
| 3 |
∵EF⊥PM,
∴∠BFH+∠HBF=90°=∠BPC+∠HBF,
∴∠BPC=∠BFH
∵EF∥NT,
∴∠NTC=∠BFH=∠BPC
tan∠NTC=tan∠BPC=
| BC |
| PC |
∴tan∠NTC=
| NC |
| CT |
∴CT=
| 5 |
| 3 |
| 5 |
| 2 |
∴k=
| 3 |
| 2 |
∴CK=2×
| 3 |
| 2 |
∵∠PKC+∠DKB=∠ABC+∠BDK,∠DKE=∠ABC,
∴∠BDK=∠PKC,
tan∠PKC=
| PC |
| KC |
∴tan∠BDK=1.
过K作KG⊥BD于G
∵tan∠BDK=1,tan∠ABC=
| 4 |
| 3 |
∴设GK=4n,则BG=3n,GD=4n
∴BK=5n=3,
∴n=
| 3 |
| 5 |
∴BD=4n+3n=7n=
| 21 |
| 5 |
∵AB=
| AC2+BC2 |
∴BQ=AB-AQ=6
∴DQ=BQ-BD=6-
| 21 |
| 5 |
| 9 |
| 5 |
解法二:

如图③,∵NP=2,PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5,AC=8,
∴AM=AP=5
∴AQ=MN=
| AM2-AN2 |
∵NM∥BC,
∴∠NMP=∠PBC
又∵∠MNP=∠BCP,
∴△MNP∽△BCP
∴
| MN |
| BC |
| NP |
| PC |
∴
| 4 |
| BC |
| 2 |
| 3 |
BC=6
作ER⊥CF于R,则四边形NERC是矩形
∴ER=NC=5,NE=CR
∵∠BHE=∠BCR=90°
∴∠EFR=90°-∠HBF∠BPC=90°-∠HBF
∴∠EFR=∠BPC,
∴tan∠EFR=tan∠BPC,
∴
| ER |
| RF |
| BC |
| PC |
| 5 |
| RF |
| 6 |
| 3 |
∴RF=
| 5 |
| 2 |
∵NE∥KC,
∴∠NEP=∠PKC
又∵∠ENP=∠KCP,
∴△NEP∽△CKP,
∴
| NE |
| KC |
| NP |
| PC |
| 2 |
| 3 |
∵CK:CF=2:3,设CK=2k,CF=3k
∴NE=CR=
| 4 |
| 3 |
| 5 |
| 2 |
∴3k-
| 5 |
| 2 |
| 4 |
| 3 |
∴k=
| 3 |
| 2 |
∴CK=3 CR=2
∴BK=3
在CF的延长线上取点G,使∠EGR=∠ABC,
∴tan∠EGR=tan∠ABC
∴
| ER |
| RG |
| AC |
| BC |
| 4 |
| 3 |
∴RG=
| 3 |
| 4 |
| 15 |
| 4 |
| ER2+RG2 |
| 25 |
| 4 |
| 35 |
| 4 |
∵∠DKE+∠EKC=∠ABC+∠BDK,∠ABC=∠DKE,
∴∠BDK=∠EKC,
∴△BDK∽△GKE,
∴
| BD |
| KG |
| BK |
| EG |
∴BD•EG=BK•KG,
∴∠BDK=∠EKC,
∴△BDK∽△GKE,
∴BD=
| 21 |
| 5 |
∵AB=
| AC2+BC2 |
∴BQ=AB-AQ=6
∴DQ=BQ-BD=6-
| 21 |
| 5 |
| 9 |
| 5 |
解法三:

如图④,∵NP=2,PC=3,
∴由(1)知PC=AN=3
∴AP=NC=5,AC=8,
∴AM=AP=5
∴AQ=MN=
| AM2-AN2 |
∵NM∥BC,
∴∠EMH=∠PBC∠PEN=∠PKC
又∵∠PNE=∠PCK,
∴△PNE∽△PCK,△PNM∽△PCB
∴
| NE |
| CK |
| PN |
| PC |
| MN |
| BC |
| PN |
| PC |
∵CK:CF=2:3,
设CK=2k,CF=3k
∴
| NE |
| 2k |
| 2 |
| 3 |
| 4 |
| BC |
| 2 |
| 3 |
∴NE=
| 4 |
| 3 |
∴BF=6+3k,ME=MN-NE=4-
| 4 |
| 3 |
tan∠ABC=
| AC |
| BC |
| 4 |
| 3 |
| PC2+BC2 |
| 5 |
∴sin∠EMH=sin∠PBC=
| PC |
| BP |
| ||
| 5 |
∵EF⊥PM,
∴FH=BFsin∠PBC=
| ||
| 5 |
EH=EMsin∠EMH=
| ||
| 5 |
| 4 |
| 3 |
∴tan∠REF=tan∠PBC=
| 1 |
| 2 |
∵tan∠REF=
| RF |
| RE |
∴RF=
| 5 |
| 2 |
∴EF=
| ER2+RF2 |
5
| ||
| 2 |
∵EH+FH=EF
∴
| ||
| 5 |
| 4 |
| 3 |
| ||
| 5 |
5
| ||
| 2 |
∴k=
| 3 |
| 2 |
∴CK=2×
| 3 |
| 2 |
∵∠PKC+∠DKE=∠ABC+∠BDK∠DKE=∠ABC,
∴∠BDK=∠PKC
∵tan∠PKC=1,
∴tan∠BDK=1,
过K作KG⊥BD于G
∵tan∠BDK=1,tan∠ABC=
| 4 |
| 3 |
∴设GK=4n,则BG=3n,GD=4n
∴BK=5n=3,
∴n=
| 3 |
| 5 |
∴BD=4n+3n=7n=
| 21 |
| 5 |
∵AB=
| AC2+BC2 |
∴BQ=AB-AQ=6,
∴DQ=BQ-BD=6-
| 21 |
| 5 |
| 9 |
| 5 |
点评:本题是几何综合题,综合考查了相似三角形、全等三角形、勾股定理、解直角三角形、角平分线性质、平行四边形、矩形等重要知识点.题干中给出的条件较多,图形复杂,难度较大,对考生能力要求较高;解题时,需要认真分析题意,以图形的相似、图形的全等为主线寻找解题思路.解答中提供了多种解题方法,可以开拓思路,希望同学们认真研究学习.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 (2012•哈尔滨)如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )
(2012•哈尔滨)如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )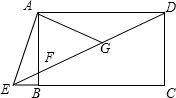 (2012•哈尔滨)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为
(2012•哈尔滨)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为