题目内容
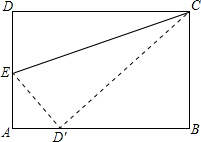 如图,取一张长方形纸片,它的长AB=10cm,宽BC=5
如图,取一张长方形纸片,它的长AB=10cm,宽BC=5| 3 |
AD上)为折痕,使D点落在AB边上,则AE=
分析:先根据翻折变换的性质及矩形的性质得到CD′=CD=AB=10,DE=ED′,由勾股定理即可求出BD′的长,进而可求出AD′的长,再设AE=x,在Rt△AED′中,利用勾股定理即可求出AE的长;再利用锐角三角函数的定义求出∠DCE的正切值即可求出∠DCE的度数.
解答:解:∵△D′CE是△DCE沿直线CE翻折而成,
∴CD′=AB=CD=10,DE=ED′,
∴在Rt△BCD′中,BD′=
=
=5,
∴AD′=AB-BD′=10-5=5,
设AE=x,则ED′=5
-x,在Rt△AED′中,AE2+AD′2=ED′2,
即x2+52=(5
-x)2,
解得x=
.
∴DE=AD-AE=5
-
=
,
∵tan∠DCE=
=
=
,
∵△CDE是直角三角形,
∴∠DCE=30°.
故答案为:
、30°.
∴CD′=AB=CD=10,DE=ED′,
∴在Rt△BCD′中,BD′=
| CD′2-BC2 |
102-(5
|
∴AD′=AB-BD′=10-5=5,
设AE=x,则ED′=5
| 3 |
即x2+52=(5
| 3 |
解得x=
5
| ||
| 3 |
∴DE=AD-AE=5
| 3 |
5
| ||
| 3 |
10
| ||
| 3 |
∵tan∠DCE=
| DE |
| CD |
| ||||
| 10 |
| ||
| 3 |
∵△CDE是直角三角形,
∴∠DCE=30°.
故答案为:
5
| ||
| 3 |
点评:本题考查的是图形翻折变换的性质,解答此类问题时首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
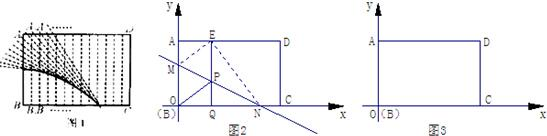



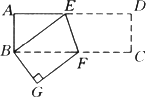
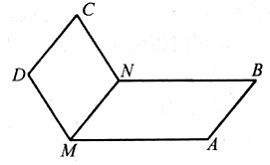
 ,若存在,写出点K的坐标;若不存在,请说明理由.
,若存在,写出点K的坐标;若不存在,请说明理由.