题目内容
【题目】已知二次函数y＝kx2+（k+1）x+1（k≠0）．
（1）求证：无论k取任何实数时，该函数图象与x轴总有交点；
（2）如果该函数的图象与x轴交点的横坐标均为整数，且k为整数，求k值．
【答案】（1）详见解析；（2）k＝±1．
【解析】
（1）根据根的判别式可得结论；
（2）利用求根公式表示两个根，因为该函数的图象与x轴交点的横坐标均为整数，且k为整数，可得k＝±1．
（1）证明：△＝（k+1）2﹣4k×1＝（k﹣1）2≥0
∴无论k取任何实数时，该函数图象与x轴总有交点；
（2）解：当y＝0时，kx2+（k+1）x+1＝0，
x＝
，
x＝
，x1＝﹣
，x2＝﹣1，
∵该函数的图象与x轴交点的横坐标均为整数，且k为整数，
∴k＝±1．
练习册系列答案
全优点练单元计划系列答案
相关题目
【题目】垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩（分） | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
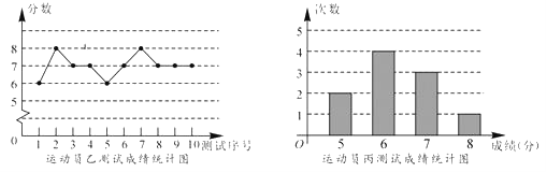
（1）写出运动员甲测试成绩的众数和中位数；
（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适?为什么?(参考数据：三人成绩的方差分别为
、
、
)
