题目内容
【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G. 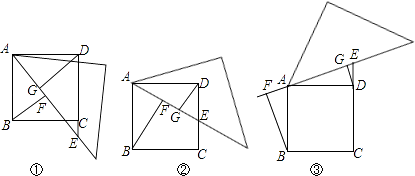
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)
【答案】
(1)证明:如图①,
∵四边形ABCD是正方形,
∴AB=AD,
∵B、D作直线AE的垂线,垂足分别为F、G.
∴∠AFB=∠DGA=90°,
∵∠BAF+∠GAD=90°,∠BAF+∠ABF=90°
∴∠ABF=∠GAD,
在△ABF和△ADG中,
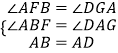 ,
,
∴△ABF≌△ADG(AAS),
∴BF=AG,AF=DG,
∵AG=AF﹣FG;
∴BF=DG﹣FG
(2)证明:如图②,
∵四边形ABCD是正方形,
∴AB=AD,
∵B、D作直线AE的垂线,垂足分别为F、G.
∴∠AFB=∠DGA=90°,
∵∠BAF+∠GAD=90°,∠BAF+∠ABF=90°
∴∠ABF=∠DAG,
在△ABF和△ADG中,
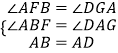 ,
,
∴△ABF≌△ADG(AAS),
∴BF=AG,AF=DG,
∵AG=AF+FG;
∴BF=DG+FG;
如图③,∵四边形ABCD是正方形,
∴AB=AD,
∵B、D作直线AE的垂线,垂足分别为F、G.
∴∠AFB=∠DGA=90°,
∵∠BAF+∠GAD=90°,∠BAF+∠ABF=90°
∴∠ABF=∠DAG,
在△ABF和△ADG中,
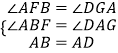 ,
,
∴△ABF≌△ADG(AAS),
∴BF=AG,AF=DG,
∵AG=FG﹣AF;
∴BF=FG﹣DG.
【解析】(1)如图①,由四边形ABCD是正方形,可得AB=AD,由B、D作直线AE的垂线,垂足分别为F、G.可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD,可得△ABF≌△ADG可得BF=AG,AF=DG,利用AG=AF﹣FG;即可证得BF=DG﹣FG;(2)如图②,由四边形ABCD是正方形,可得AB=AD,由B、D作直线AE的垂线,垂足分别为F、G.可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD,可得△ABF≌△ADG可得BF=AG,AF=DG,利用AG=AF+FG,可得BF=DG+FG;如图③,由四边形ABCD是正方形,可得AB=AD,由B、D作直线AE的垂线,垂足分别为F、G.可得∠AFB=∠DGA=90°由角的关系可得∠ABF=∠GAD,可得△ABF≌△ADG可得BF=AG,AF=DG,利用AG=FG﹣AF,可得BF=FG﹣DG.

 字词句段篇系列答案
字词句段篇系列答案